Grafik Fungsi Trigonometri - Grafik dari tiga fungsi trigonometri yang utama adalah sinus, cosinus dan tangen.
Fungsi Sinus
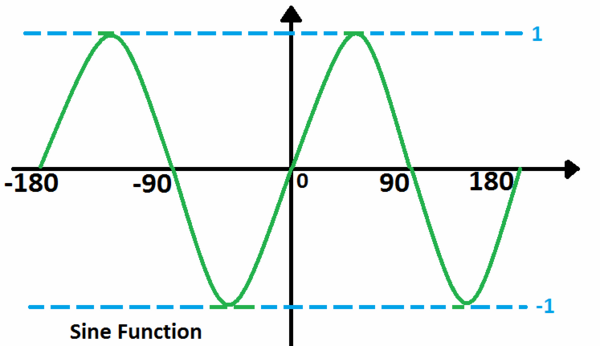
Grafik sinus adalah periodik dengan periode 360∘ atau 2π
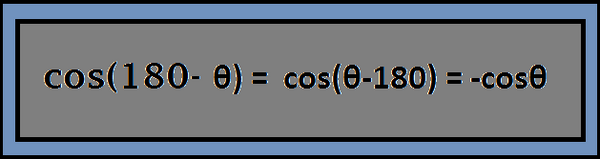
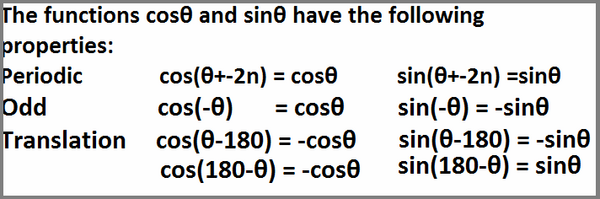

Tentang:
Matematika
 |
| Grafik Fungsi Trigonometri |
Fungsi Sinus
Grafik sinus adalah periodik dengan periode 360∘ atau 2π
Juga terletak pada dan termasuk -1 and 1.
- Grafik berlanjut tanpa keterlambatan
- Kisarannya adalah −1≤sinx≤+1
- Bentuk grafik dari x = 0 to x = 2n diulangi setiap radian 2n radian contoh, ini mempunyai periode 2n atau 360∘.( n menandakan nilai satu pie sama dengan 180∘)
- Ini disebut fungsi  periodik atau putaran;dan total lebar dari pola terulang diukur dalam aksis horisontal disebut periode. Gelombang sinus memiliki periode 2n, nilai maksimum +1 dan nilai minimum -1.
- Nilai terbesar dari gelombang sinus disebut amplitudo.
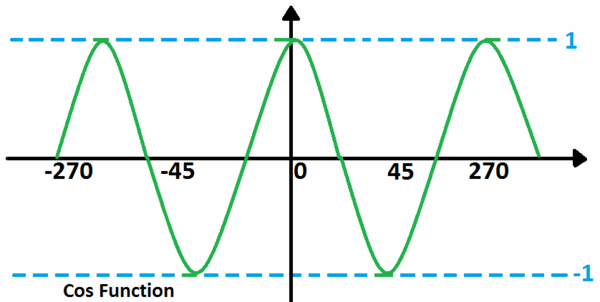
Fungsi cosinus
Grafik berkelanjutan tanpa keterlambatan seperti fungsi sinus, dengan sedikit perbedaan yang diuraikan di bawah ini:
Grafik berkelanjutan tanpa keterlambatan seperti fungsi sinus, dengan sedikit perbedaan yang diuraikan di bawah ini:
- Kisaran −1≤cosx≤+1
- memiliki periode 2n contoh, 360∘ atau 2n.
- Bentuknya sama dengan gelombang sinus tetapi keterlambatan jarak n/2 ke kiri pada aksis horisontal.
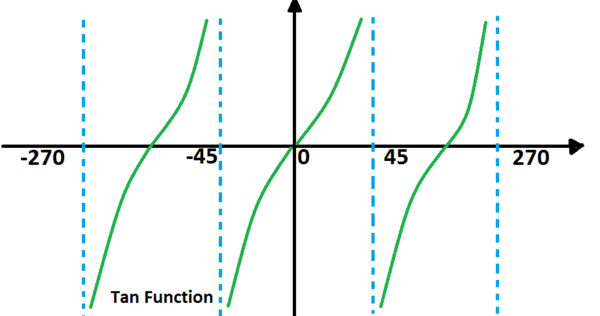
Fungsi tangen
- Fungsi tangen ditemukan dengan menggunakan -> tanθ = sinθ/cosθ
- Karenanya, grafik tanθ didefinisikan ketika sinθ = 0. Maka, tanθ = 0, tetapi ini tak terdefinisi ketika cosθ = 0.
Kisaran nilai untuk tidak terbatas.
Ini memiliki periode n.
Melanjutkan dari tiga fungsi utama di atas Anda akan melihat bahwa setiap dari mereka mempunyai beberapa karakteristik simetrik.
Grafik adalah simetri terhadap aksis vertikal. Jika Anda menggantikannya dengan - akan tetap sama.
Jadi, cos(-θ) = cosθ
Grafik adalah simetri terhadap aksis vertikal. Jika Anda menggantikannya dengan - akan tetap sama.
Jadi, cos(-θ) = cosθ
Dan, cos(θ-180) = -cosθ
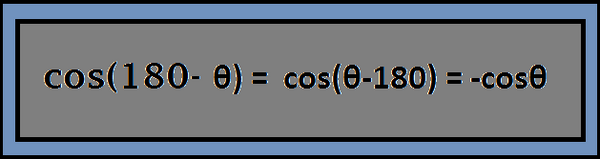
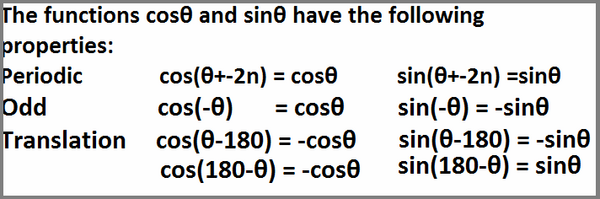
Jika Anda melihat kembali pada grafik tanθ, ini memiliki karakteristik yang sama seperti grafik sinus dan cosinus.

Jika sebuah grafik diperbesar ia akan dinotasikan dengan sebuah angka penuh yang ditulis pada sisi kiri fungsi.
Contoh 1
Contoh 1
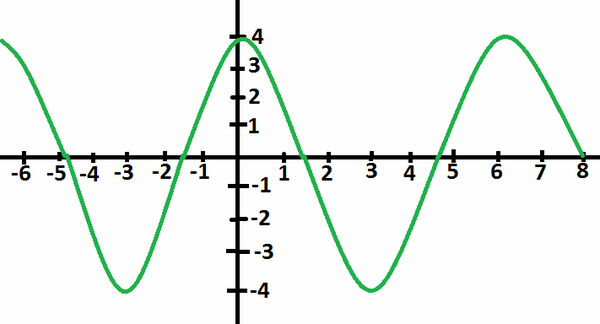
Mensketsa sebuah grafik 4 cos(x/4)
Di sini, 4 adalah perbesaran dan (x/4) adalah periode fungsi.
Catatan bahwa periode standar grafik cosinus adalah 2n so
(x/4) = 2n,
--> x = 8n
karenanya, tidak ada keterlambatan pada sistem ataupun pada konstan yang ditambahkan apapun. Grafik akan serupa dengan grafik standar cos(x) dengan perbesaran hingga 4 dan periode diperbesar hingga 8n.
Di sini, 4 adalah perbesaran dan (x/4) adalah periode fungsi.
Catatan bahwa periode standar grafik cosinus adalah 2n so
(x/4) = 2n,
--> x = 8n
karenanya, tidak ada keterlambatan pada sistem ataupun pada konstan yang ditambahkan apapun. Grafik akan serupa dengan grafik standar cos(x) dengan perbesaran hingga 4 dan periode diperbesar hingga 8n.
Contoh 2
Mengidentifikasi grafik tan (x/2 + n)
Dengan menggunakan karakteristik periodik tan dalam kasus ini tan(θ+2n) = tanθ
Anda mendapat tan(x/2 + n) = tan (x/2)
Sekarang, periode tan (x/2) ditentukan sebagai berikut
x/2 = n, maka x = 2n
Jadi, f(x) akan sama dengan grafik tan(x) tetapi dengan periode ganda (2n) sebagai ganti n.
Contoh 3
Yang mana dari grafik berikut merupakan f(x) = 2sin(-x+3)
Penjelasan
Dengan menggunakan karakteristik ganjil dari fungsi sinus, sin(-θ) = sinθ
jadi sin (-(x+3)) = -sin(x+3) = f(x)
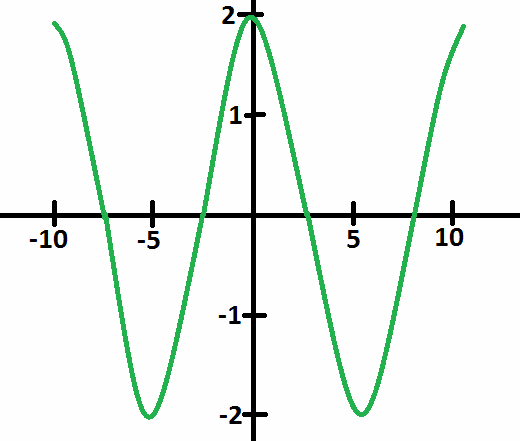
Pertama, 2sin(x+3) akan sama dengan 2sin(x) bergeser 3 unit ke kiri, ini akan melewati dari awal pada x = -3 daripada x = 0.
Mengidentifikasi grafik tan (x/2 + n)
Dengan menggunakan karakteristik periodik tan dalam kasus ini tan(θ+2n) = tanθ
Anda mendapat tan(x/2 + n) = tan (x/2)
Sekarang, periode tan (x/2) ditentukan sebagai berikut
x/2 = n, maka x = 2n
Jadi, f(x) akan sama dengan grafik tan(x) tetapi dengan periode ganda (2n) sebagai ganti n.
Contoh 3
Yang mana dari grafik berikut merupakan f(x) = 2sin(-x+3)
Penjelasan
Dengan menggunakan karakteristik ganjil dari fungsi sinus, sin(-θ) = sinθ
jadi sin (-(x+3)) = -sin(x+3) = f(x)
Pertama, 2sin(x+3) akan sama dengan 2sin(x) bergeser 3 unit ke kiri, ini akan melewati dari awal pada x = -3 daripada x = 0.
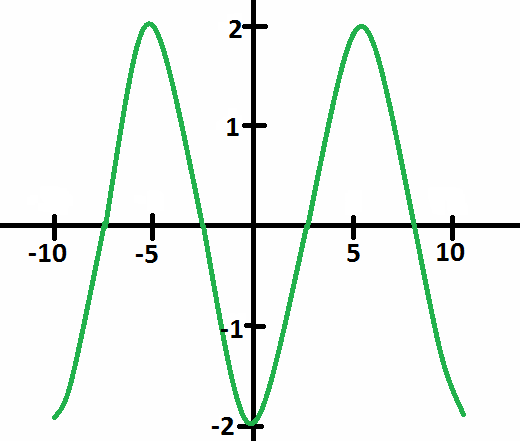
Karena itu, sin(-x+3) = -sin(x+3)
dengan demikian akan menjadi gambar yang terinvers mengenai aksis x dari 2sin(x+3) seperti yang ditunjukkan di bawah.
dengan demikian akan menjadi gambar yang terinvers mengenai aksis x dari 2sin(x+3) seperti yang ditunjukkan di bawah.






Tidak ada komentar:
Posting Komentar