Contoh Soal Penerapan Sifat-sifat Irisan Dua Lingkaran - Sebelum mempelajari topik ini, mari kita ingat kembali beberapa hal berikut ini :
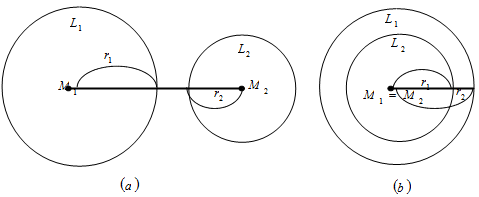
(3) Panjang garis singgung persekutuan dalam adalah panjang ruas garis yang dibentuk oleh titik-titik singgung lingkaran dengan garis singgung persekutuan dalam.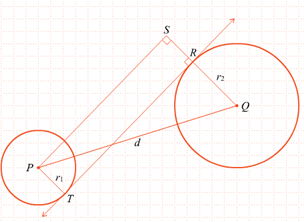
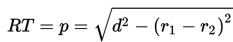
(4) “Kuadrat dari panjang ruas garis singgung persekutuan luar dua lingkaran sama dengan kuadrat dari jarak titik pusat kedua lingkaran dikurangi dengan kuadrat dari selisih jari-jarinya”.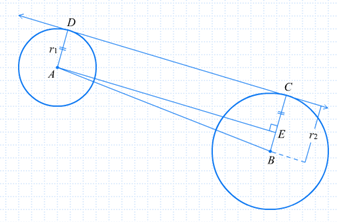
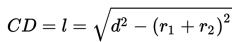
Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1
Penyelesaian :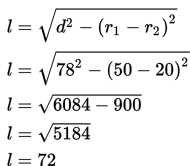
Contoh 2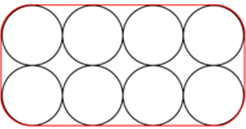
Penyelesaian :
Contoh 3
Penyelesaian :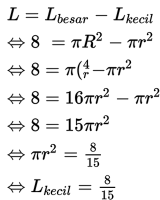
Contoh 4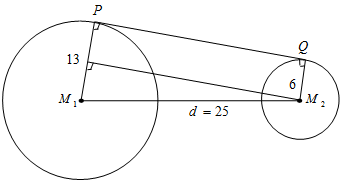
Penyelesaian :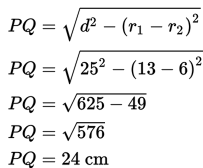

π cm 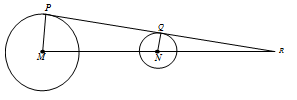
Tentang:
MIA kelas 11
(1) Lingkaran adalah himpunan titik-titik yang berjarak sama terhadap suatu titik tertentu.
(2) Kedudukan dua lingkaran
Jika M1M2 merupakan jarak antara dua pusat lingkaran dan r1 dan r2 merupakan jari-jari kedua lingkaran, maka :
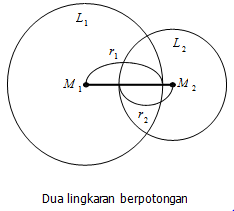
Dua lingkaran dikatakan berpotongan jika jarak antara kedua titik pusat lingkaran
M1M2 < r1 + r2
M1M2 < r1 + r2

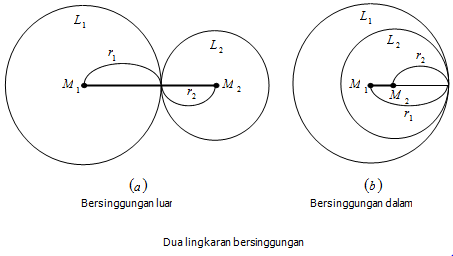
Dua lingkaran dikatakan bersinggungan luar jika jarak antara kedua titik pusat lingkaran M1M2 = r1 + r2
Dua lingkaran dikatakan bersinggungan dalam jika jarak antara kedua titik pusat lingkaran M1M2 = |r1 - r2|

Dua lingkaran dikatakan tidak bersinggungan luar jika jarak antara kedua titik pusat lingkaran M1M2 > r1 + r2
Dua lingkaran dikatakan tidak bersinggungan dalam jika jarak antara kedua titik pusat lingkaran adalah nol (M1M2 = 0 -> M1 = M2) dan r2 > r1
Namun perlu diketahui juga, dua lingkaran dapat tidak bersinggungan dalam jika salah satu lingkaran berada di dalam lingkaran yang lain, M1 ≠ M2 dan r2 > r1
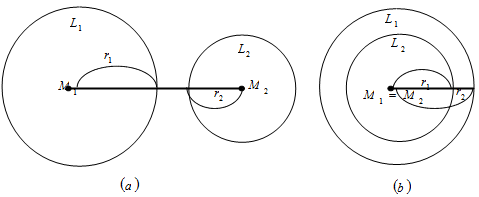
(3) Panjang garis singgung persekutuan dalam adalah panjang ruas garis yang dibentuk oleh titik-titik singgung lingkaran dengan garis singgung persekutuan dalam.
“Kuadrat dari panjang garis singgung persekutuan dalam lingkaran sama dengan kuadrat dari jarak titik-titik pusat kedua lingkaran dikurangi dengan kuadrat dari jumlah panjang jari-jarinya”.

Panjang garis singgung persekutuan luar dua lingkaran yang memiliki jari-jari r1 dan r2 dengan r1 > r2 , serta jarak kedua pusat lingkaran d adalah :
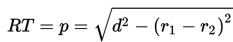
(4) “Kuadrat dari panjang ruas garis singgung persekutuan luar dua lingkaran sama dengan kuadrat dari jarak titik pusat kedua lingkaran dikurangi dengan kuadrat dari selisih jari-jarinya”.

Panjang garis singgung persekutuan dalam dua lingkaran yang memiliki jari-jari r1 dan r2, serta jarak kedua pusat lingkaran d adalah :
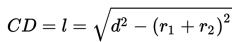
Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1
Dua buah roda sepeda yang jarak kedua porosnya adalah 78 cm, roda pertama memiliki panjang jari-jari 50 cm dan roda kedua 20 cm. Pada kedua roda dipasang rantai. Tentukan panjang rantai yang tidak menempel pada roda!
Penyelesaian :
Permasalahan di atas merupakan penerapan dari konsep garis singgung persekutuan luar dua lingkaran.
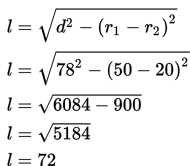
Jadi, panjang rantai yang tidak menempel pada roda sepeda adalah 8 cm.
Contoh 2
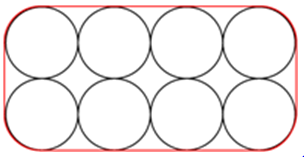
Sebanyak 8 buah tabung disusun seperti pada gambar di samping, kemudian diikat dengan seutas tali. Jika panjang jari-jari tabung 14 cm, maka tentukan panjang tali terpendek yang digunakan untuk mengikat tabung-tabung tersebut!

Penyelesaian :
- Jarak pusat dua lingkaran = diameter lingkaran = 28 cm
- Jumlah panjang tali di sudut-sudut tabung = keliling lingkaran = πd = 88 cm
Jadi, panjang tali terpendek yang digunakan untuk mengikat tabung adalah :
(8 x 28 cm) + 88 cm = 312 cm
(8 x 28 cm) + 88 cm = 312 cm
Contoh 3
Dua lingkaran pada bidang mempunyai titik pusat yang sama. Jari-jari lingkaran besar adalah empat kali jari-jari lingkaran kecil. Jika luas daerah di antara kedua lingkaran adalah 8 satuan luas, hitunglah luas daerah lingkaran kecil.
Penyelesaian :
Misalkan jari-jari lingkaran besar = R dan jari-jari lingkaran kecil = r sehingga diperoleh
R = 4r
R = 4r
Dengan demikian,
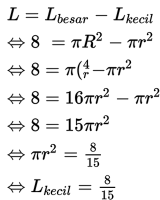
Jadi, luas daerah lingkaran kecil adalah 8/15 satuan luas.
Contoh 4
Pak Agus sedang merancang sebuah gerobak seperti tampak pada gambar di bawah ini.

Pada salah satu sisi gerobak tersebut terdapat sebuah papan berbentuk trapesium yang menghubungkan kedua roda gerobak. Apabila jari-jari roda yang besar adalah r1 = 13 cm, jari-jari roda yang kecil adalah r2 = 6 cm, jarak titik pusat roda L1 dan roda L2adalah M1M2 = 25 cm, maka berapakah luas papan yang menghubungkan kedua roda tersebut?
Penyelesaian :
Kita hitung terlebih dahulu panjang garis singgung persekutuan luar PQ.
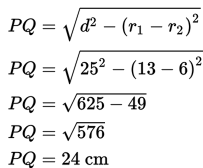
Adapun luas trapesium PM1M2Q adalah

Jadi, luas papan penghubung kedua roda tersebut adalah 228 cm2
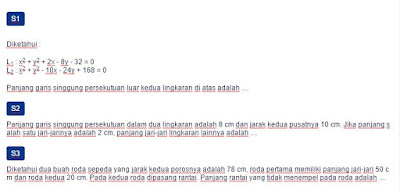
S1
Diketahui :
L1 : x2 + y2 + 2x - 8y - 32 = 0
L2 : x2 + y2 - 10x - 24y + 168 = 0
L2 : x2 + y2 - 10x - 24y + 168 = 0
Panjang garis singgung persekutuan luar kedua lingkaran di atas adalah ....
S2
Panjang garis singgung persekutuan dalam dua lingkaran adalah 8 cm dan jarak kedua pusatnya 10 cm. Jika panjang salah satu jari-jarinya adalah 2 cm, panjang jari-jari lingkaran lainnya adalah ....
S3
Diketahui dua buah roda sepeda yang jarak kedua porosnya adalah 78 cm, roda pertama memiliki panjang jari-jari 50 cm dan roda kedua 20 cm. Pada kedua roda dipasang rantai. Panjang rantai yang tidak menempel pada roda adalah ....
S4
Diketahui :
L1 : x2 + y2 + 2x - 2y - 7 = 0
L2 : x2 + y2 - 6x + 12y + 41 = 0
L2 : x2 + y2 - 6x + 12y + 41 = 0
Panjang garis singgung persekutuan dalam kedua lingkaran di atas adalah ....
S5
Dua lingkaran pada bidang mempunyai titik pusat yang sama. Jari-jari lingkaran besar adalah tiga kali jari-jari lingkaran kecil. Jika luas daerah di antara kedua lingkaran adalah 8 satuan luas, maka luas daerah lingkaran kecil adalah...
S6
Sebanyak 8 buah tabung disusun seperti pada gambar di samping, kemudian diikat dengan seutas tali. Jika panjang jari-jari tabung 14 cm, maka panjang tali terpendek yang digunakan untuk mengikat tabung-tabung tersebut adalah...

S7
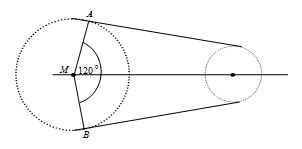
Perhatikan gambar di bawah. Rantai sepeda dipasang pada lingkaran pemutarnya. Panjang jari-jari lingkaran pada roda gigi depan 14 cm dan panjang jari-jari lingkaran pemutar roda gigi belakang 3,5 cm. Jika jarak antara kedua pusat lingkaran tersebut 21 cm dan besar sudut AMB = 120o , panjang rantai sepeda tersebut adalah ....

S8
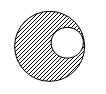
Perhatikan gambar berikut.

Luas daerah yang diarsir adalah 4 kali luas daerah lingkaran kecil. Jika jari-jari lingkaran besar adalah
maka keliling lingkaran kecil dan jarak antara kedua pusat lingkaran berturut-turut adalah ....
S9
Diketahui MP=9 cm, PQ=20 cm dan MN=25 cm, perbandingan luas lingkaran yang berpusat di N terhadap lingkaran berpusat di M adalah....
S10
Perhatikan gambar di bawah. PQ adalah garis singgung persekutuan luar dua lingkaran. Jika jari-jari lingkaran M =12 cm, jari-jari lingkaran N = 3 cm, dan MR = 20 cm, maka panjang PR adalah ....

Tidak ada komentar:
Posting Komentar