Contoh Soal Persamaan Logaritma Berbentuk ^a log f(x) = ^a log p - Persamaan logaritma adalah suatu persamaan yang variabelnya terletak pada numerus atau pada bilangan pokok atau pada keduanya dari suatu logaritma. Perhatikan contoh persamaan berikut:

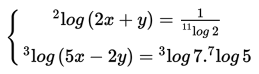
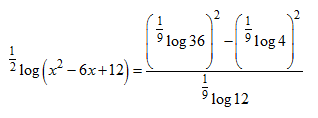
Tentang:
Matematika Ipa kelas 12
- Bentuk log (2x + 1) + log x = 1, merupakan persamaan logaritma dengan variabel x terletak pada numerus.
- Bentuk x log 2 + x log 3 = 5, merupakan persamaan logaritma dengan variabel x terletak pada bilangan pokok.
- Bentuk 2y log (2y + 1) - 2y log y = -2, merupakan persamaan logaritma dengan variabel y terletak pada numerus dan pada bilangan pokok.
Pada topik ini, kita akan belajar menentukan penyelesaian dari persamaan logaritma dengan variabel terletak pada numerus dari suatu logaritma, yaitu berbentuk a log f(x) = a log p. Cara menyelesaikan persamaan tersebut adalah dengan menentukan nilai variabel yang menyebabkan persamaan menjadi pernyataan yang bernilai benar, yaitu:
Jika a log f(x) = a log p, f(x) > 0, maka f(x) = p
SOAL 1
Jika log (2x2 + x) = 0, maka nilai x yang memenuhi adalah ….
SOAL 2
Nilai x yang memenuhi persamaan log (x + 5) = log x + log 5 adalah ….
SOAL 3
Diketahui persamaan . Untuk nilai x yang memenuhi persamaan tersebut, nilai dari = ….
SOAL 4
Himpunan penyelesaian dari persamaan 7 log (x + 1) + 7 log (x - 5) = 1 adalah {x₁, x₂}. Nilai dari x₁ + x₂ = ….
SOAL 5
Hasil kali akar-akar persamaan logaritma 2 log (x2– 3x) = 2 adalah ….
SOAL 6
Penyelesaian dari persamaan logaritma log (2x2– 11x + 22) = 5 log + 5 log 20 - 5 log 2 adalah x₁ dan x₂. Jika x₁ < x₂, nilai 2x₁ - x₂ adalah ….
SOAL 7
Hasil kali akar-akar persamaan logaritma 2 log (x - 2) + 2 log (x - 3) = 2 log 5. 5 log 3 adalah ….
SOAL 8
Diketahui persamaan logaritma:

Nilai dari x + y adalah ….
SOAL 9
Nilai x + y yang memenuhi sistem persamaan logaritma berikut:
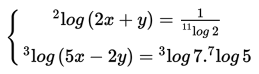
adalah ….
SOAL 10
Penyelesaian persamaan
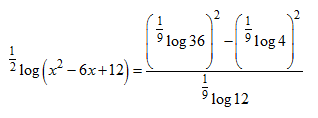
adalah x₁ dan x₂. Jika x₁ < x₂, maka nilai x₂ log x₁ adalah ….

Tidak ada komentar:
Posting Komentar