Contoh Soal Persamaan Eksponen Berbentuk h(x)^f(x) = h(x)^g(x)

Contoh Soal Persamaan Eksponen Berbentuk h(x)^f(x) = h(x)^g(x) - Persamaan eksponen adalah persamaan yang pangkatnya memuat peubah (variabel) atau bilangan pokok dan pangkatnya sama-sama memuat peubah (variabel). Pada topik sebelumnya, kamu telah mempelajari penyelesaian dari 4 macam bentuk persamaan eksponen diantaranya:

1). Persamaan eksponen berbentuk af (x) = 1
2). Persamaan eksponen berbentuk af (x) = ap
3). Persamaan eksponen berbentuk af (x) = bf (x)
4). Persamaan eksponen berbentuk af (x) = ag (x)

       Pada materi kali ini, kamu akan mempelajari tentang persamaan eksponen yang bilangan pokok dan pangkatnya memuat fungsi (peubah/variabel) yaitu persamaan eksponen berbentuk [h (x)]f (x) = [h (x)]g (x). Sebagaimana halnya persamaan-persamaan eksponen sebelumnya, kamu juga dapat menentukan himpunan penyelesaian dari persamaan eksponen berbentuk [h (x)]f (x) = [h (x)]g (x).

SOAL 1

Himpunan penyelesaian dari persamaan eksponen (x - 6)2x - 4 = (x - 6)2 - x adalah ....

SOAL 2

Diketahui persamaan eksponen (x - 7)2x - 9 = (x - 7)x+ 5. Nilai x yang memenuhi adalah ....

SOAL 3

Himpunan penyelesaian dari persamaan (5x - 2)x- 5 = (5x - 2)2x + 1 adalah ....

SOAL 4

Himpunan penyelesaian dari persamaan (x2 - 1)x + 2 = (x2 - 1)2x - 1 adalah ...

SOAL 5

Himpunan penyelesaian dari persamaan (x - 5)x2 – 4 = (x - 5)2 – x adalah ....

SOAL 6

Himpunan penyelesaian dari persamaan (x2 )x = x4x - x2 adalah ....

SOAL 7

Himpunan penyelesaian dari persamaan
(2x - 5)x2 + 1 = (2x - 5)x + 7
adalah ....

SOAL 8

Himpunan penyelesaian dari persamaan
(x2 – 3x + 1)x + 3 = (x2 – 3x + 1)x2 - 3
adalah ....

SOAL 9

Himpunan penyelesaian dari persamaan

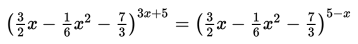
adalah ....

SOAL 10

Himpunan penyelesaian dari persamaan
(x2 – 3x + 1)x2 + 3x - 4 = (x2 – 3x + 1)4x + 2
adalah ....

Tentang: Matematika Ipa kelas 12

Share:

Artikel Terkait