Contoh Soal Persamaan Eksponen Berbentuk a^f(x) = a^g(x) - Pada topik sebelumnya, kamu telah memahami bahwa cara untuk menentukan himpunan penyelesaian dari persamaan eksponen adalah berbeda-beda, sesuai dengan bentuk persamaan eksponennya. Hal tersebut dikarenakan oleh bentuk persamaan eksponen yang tidak tunggal. Persamaan eksponen dapat berupa persamaan yang eksponennya memuat variabel atau berupa persamaan yang bilangan pokok dan eksponennya memuat variabel.
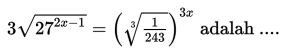
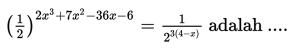
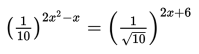
Tentang:
Matematika Ipa kelas 12
Kamu telah belajar tentang persamaan eksponen yang salah satu eksponenya memuat variabel dengan bilangan pokok yang sama yaitu af(x) = 1 atau af(x) = ap . Kamu juga telah belajar tentang persamaan eksponen dengan bilangan pokok yang berbeda dan eksponennya memuat variabel yang merupakan sebuah fungsi yang sama yaitu af(x)= bf(x) . Pada topik kali ini, kamu akan belajar tentang persamaan eksponen dengan bilangan pokok yang sama dan eksponennya memuat variabel yang merupakan fungsi yang berbeda, yaitu af(x) = ag(x) .
Seperti halnya menentukan himpunan penyelesaian dari persamaan-persamaan eksponen sebelumnya, kamu juga dapat menentukan himpunan penyelesaian dari persamaan eksponen berbentuk af(x) = ag(x) . Untuk memudahkanmu dalam menentukan himpunan penyelesaian dari persamaan eksponen berbentuk af(x) = ag(x) , maka tidak ada salahnya jika kamu mengingat kembali penyelesaian dari beberapa contoh soal berikut yang berkaitan dengan persamaan eksponen berbentuk af(x) = bf(x) yang telah kalian pelajari sebelumnya.
SOAL 1
Diketahui persamaan eksponen 255x-3 – 125x+2 = 0. Himpunan penyelesaian dari persamaan tersebut adalah ...
SOAL 2
Himpunan penyelesaian dari persamaan adalah ....
SOAL 3
Nilai x yang memenuhi persamaan adalah ....
SOAL 4
Nilai x yang memenuhi persamaan:
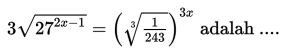
SOAL 5
Himpunan penyelesaian dari persamaan adalah ....
SOAL 6
Akar-akar penyelesaian dari persamaan adalah x₁ dan x₂. Jika x₁ > x₂, maka nilai dari x₁ - x₂ adalah ....
SOAL 7
Nilai x yang memenuhi persamaan adalah ....
SOAL 8
Jika dan , bilangan asli, maka = ….
SOAL 9
Akar-akar penyelesaian dari persamaan:
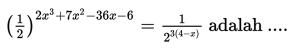
SOAL 10
x₁ dan x₂ adalah akar-akar persamaan:
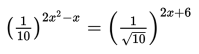
Nilai dari (x₁ - x₂)2 adalah ....

Tidak ada komentar:
Posting Komentar