Contoh Soal Penerapan Relasi dan Fungsi dalam Kehidupan Sehari-Hari

Contoh Soal Penerapan Relasi dan Fungsi dalam Kehidupan Sehari-Hari - Pada topik-topik sebelumnya, kita telah mempelajari tentang relasi dan fungsi. Melalui topik ini, kita akan membahas tentang penerapan relasi dan fungsi dalam kehidupan sehari-hari. Agar kamu lebih paham tentang penerapan relasi dan fungsi dalam kehidupan sehari-hari, mari kita ingat kembali tentang pengertian relasi, fungsi, korepondensi satu-satu, cara menyajikan suatu relasi dan fungsi, menghitung nilai fungsi, dan grafik fungsi.

Pengertian Relasi

Relasi dari himpunan A ke himpunan B adalah suatu aturan yang memasangkan anggota-anggota himpunan A dengan anggota-anggota himpunan B. Relasi dapat disajikan dalam diagram panah, diagram cartesius , ataupun dalam himpunan pasangan berurutan.

Pengertian Fungsi

Fungsi (pemetaan) dari himpuan A ke himpunan B adalah relasi khusus yang memasangkan setiap anggota A dengan tepat satu anggota himpunan B.

Pengertian korespondensi satu-satu

Korespondensi satu-satu adalah fungsi yang memetakan setiap anggota dari himpunan A ke satu anggota B dan setiap anggota dari himpuan B ke satu anggota A. Jadi, banyak anggota himpunan A dan B harus sama atau n (A) = n (B).

Cara Menyajikan Suatu Relasi dan Fungsi

Cara menyajikan suatu relasi dan fungsi yaitu dengan:

• diagram panah
• diagram Kartesius
• himpunan pasangan berurutan

Menghitung Nilai Fungsi

Nilai fungsi dapat dihitung dengan menggunakan tabel fungsi. Tabel fungsi memuat anggota-anggota daerah asal (domain) dan bayangannnya.

Grafik Fungsi

Pada materi relasi dan fungsi, kita dapat menggambar grafik fungsi linear dan kuadrat. Grafik fungsi linear berbentuk garis lurus dan grafik fungsi kuadrat menyerupai parabola.

Relasi dan fungsi umumnya digunakan untuk menyatakan hubungan antara dua atau beberapa objek. Contoh penerapannya adalah sebagai berikut.

• Silsilah Keluarga
  Pada silsilah keluarga, kita dapat membentuk beberapa relasi antaranggota keluarga, misalnya hubungan ayah dan anak, serta hubungan antarsaudara.
• Negara dan ibukota negaranya.
• Siswa dalam suatu kelas dengan peringkat kelasnya.

       Masih banyak lagi contoh penerapan relasi dan fungsi dalam kehidupan sehari-hari. Dalam matematika, persoalan mengenai penerapan relasi dan fungsi dalam kehidupan sehari-hari biasa disajikan dalam bentuk soal cerita dengan berbagai variasi. Salah satu bentuk variasi soal penerapan relasi dan fungsi dapat diselesaikan dengan langkah-langkah sebagai berikut.

• Tentukan domain dan kodomain dari soal cerita.
• Nyatakan relasi dengan diagram panah, diagram cartesius atau himpunan pasangan berurutan.
• Tentukan jawaban berdasarkan diagram panah, diagram cartesius atau himpuan pasangan berurutan yang telah dibuat.

✎Contoh Soal

Ayah menabung di Bank dengan tabungan awal Rp500.000,00. Jika ayah rutin menabung setiap bulan dengan besar yang sama dengan tabungan awal, maka jumlah tabungan ayah pada bulan ke-6 adalah ...

Penyelesaian:

Misalkan:
x = lama menabung (dalam bulan)
f (x) = jumlah tabungan ayah pada bulan ke-x

Oleh karena tabungan ayah bertambah sebanyak Rp500.000,00 setiap bulan, maka:
f (x) = 500.000x

Untuk menentukan jumlah tabungan ayah pada bulan ke-6, substitusikan x = 6 ke f (x), sehingga:

f (x) = 500.000x
⇔ f (6) = 500.000(6) = 3.000.000

Jadi, jumlah tabungan ayah pada bulan ke-6 adalah Rp3.000.000,00.

S1

Pilihan Tunggal

Dalam suatu kelas, empat orang murid memilih kegiatan ekstrakurikuler yang akan diikuti. Keempat murid tersebut adalah Aqila, Haikal, Raka, dan Karla. Aqila memilih kegiatan pramuka dan paskibra. Haikal memilih kegiatan bola basket. Raka memilih kegiatan sepak bola dan pramuka. Karla meilih kegiatan paskibra dan bola basket. Diagram Kartesius yang menunjukan relasi “memilih ekstrakurikuler” dari himpunan murid ke himpunan kegiatan ekstrakuriler adalah ....

S2

Pilihan Tunggal

Diketahui pernyataan-pernyataan berikut.

(1) Siswa dengan tempat duduknya.
(2) Penonton pertandingan sepak bola dengan tiket masuknya.
(3) Siswa dengan daftar hadirnya.
(4) Semua siswa dengan guru-guru di suatu sekolah.

Pernyataan yang merupakan contoh korespondensi satu-satu adalah ....

S3

Pilihan Tunggal

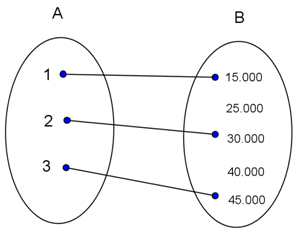
Perhatikan diagram panah berikut.

Diagram panah diatas menunjukan fungsi yang memiliki relasi “jumlah tabungan” dari himpunan A ke himpunan B. Jika A = {1, 2, 3}, B ={15.000, 25.000, 30.000, 40.000, 45.000}, maka kodomain dari fungsi yang ditunjukan oleh diagram panah tersebut adalah ....

S4

Pilihan Tunggal

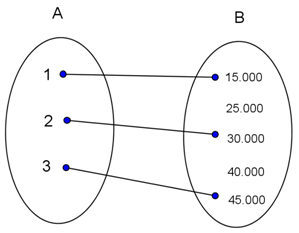
Perhatikan diagram panah berikut.

Diagram panah tersebut mencerminkan harga dari baju kemeja merek 1, 2, dan 3. Himpunan pasangan berurutan dari fungsi yang terbentuk adalah ...

S5

Pilihan Tunggal

Ibu berbelanja keperluan rumah tangga untuk 3 hari berturut-turut sejumlah Rp300.000,00. Jumlah uang yang sudah dikeluarkan Ibu untuk 2 hari adalah ....

S6

Pilihan Tunggal

Bu Ida mengeluarkan uang untuk berbelanja keperluan rumah tangga selama 3 hari berturut-turut sejumlah Rp300.000,00. Banyak fungsi yang mungkin dari himpunan “hari ke-x Bu Ida berbelanja“ ke himpunan “jumlah uang sudah dikeluarkan Bu Ida adalah ....

S7

Pilihan Tunggal

Nilai Matematika Ana setiap semester selalu mengalami peningkatan sebanyak 2 poin. Sekarang, Ana merupakan siswa kelas 9 semester I. Jika nilai matematika Ana pada kelas 7 semester II adalah 84, maka nilai Ana pada kelas 8 semester II adalah ....

S8

Pilihan Tunggal

Nilai Matematika Nino selalu mengalami peningkatan sebanyak 2 poin setiap semester. Saat ini, Nino merupakan siswa kelas 9 semester I. Jika nilai Matematika Nino pada kelas 7 semester II adalah 84, maka gambar grafik fungsi nilai Matematika Nino selama 4 semester adalah ....

S9

Pilihan Tunggal

Grafik penerimaan siswa di suatu sekolah dalam ujian masuk SMA negeri selalu meningkat dari tahun ke tahun, sehingga dinyatakan dalam fungsi y = 4x + 1. Grafik fungsinya adalah ....

S10

Pilihan Tunggal

Fandi menembakkan sebuah batu dengan ketapel sehingga membentuk suatu grafik fungsi f (x) = -x2 + 9, maka grafik fungsinya adalah ....

Tentang: Matematika

Share:

Artikel Terkait