Contoh Soal Teorema Pythagoras pada Sisi-Sisi Segitiga Siku-Siku - Seorang nelayan mendayung perahunya sejauh 50 km ke arah timur. Kemudian, memutar haluan sejauh 120 km ke arah selatan. Tahukah kamu berapa kilometer jarak perahu tersebut sekarang dari tempatnya berangkatnya? Untuk mengetahuinya, kamu dapat menerapkan teorema Pythagoras, sebuah teorema yang sangat terkenal. Bagaimana caranya? Mari kita pelajari bersama.





Tentang:
Matematika

A. Mengingat Kembali Teorema Pythagoras
Pada topik sebelumnya, kamu sudah mempelajari tentang teorema Pythagoras, yaitu sebagai berikut.

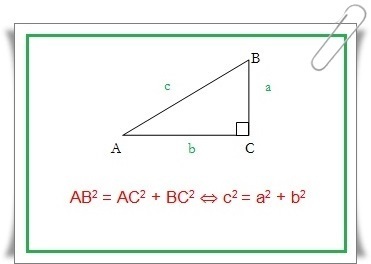
Misalnya, pada ∆ABC yang siku-siku di C, berlaku:

●●●●Contoh 1●●●●
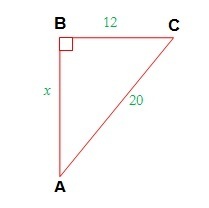
Coba tentukan nilai x pada bangun berikut.

Jawab:
Dapat kamu amati bahwa ∆ABC siku-siku di B sehingga:
AC2 = AB2 + BC2
⇔ 202 = x2 + 122
⇔400 = x2 + 144
⇔x2 = 400 – 144
⇔x2 = 256
⇔x =
⇔x = 16
Jadi, x = 16.
B. Tripel Pythagoras
Untuk menentukan salah satu sisi pada segitiga siku-siku dengan cepat dapat dilakukan dengan mudah dan tanpa menggunakan teorema Pythagoras. Caranya kamu dapat menggunakan tripel Pythagoras.

Berikut ini daftar tripel Pythagoras.

Pasangan tripel ini berlaku untuk kelipatannya.
●●●●Contoh 2●●●●
Buktikan bahwa 12, 5, 13 merupakan tripel Pythagoras.
Jawab:
Misalkan a = 12, b = 5, dan c = 13.
Berarti, a2 = 144, b2 = 25, dan c2 = 169.
Kamu dapat mengamati bahwa a2 + b2 = 144 + 25 = 169.
Jadi, c2 = a2 + b2 .
Ini berarti, 12, 5, 13 memenuhi teorema Pythagoras sehingga ketiga bilangan tersebut merupakan tripel Pythagoras.
C. Menentukan Jenis Segitiga jika Diketahui Panjang Sisi-Sisinya
Menurut teorema Pythagoras, pada ∆ABC yang siku-siku di C, berlaku c2 = a2 + b2 . Pernyataan tersebut berlaku juga sebaliknya, yaitu jika pada ∆ABC diketahui c2 = a2 + b2 maka ∆ABC merupakan segitiga siku-siku di C. Kebalikan teorema Pythagoras ini dapat digunakan untuk menyelidiki apakah sebuah segitiga merupakan segitiga siku-siku atau bukan.
Selengkapnya mengenai jenis-jenis segitiga jika diketahui panjang sisinya, yaitu sebagai berikut.

●●●●Contoh 3●●●●
Coba selidiki apakah ∆ABC dengan panjang sisi 15 cm, 36 cm, dan 39 cm merupakan segitiga siku-siku.
Jawab:
Sisi terpanjang pada ∆ABC memiliki panjang 39 cm. Kamu dapatkan 392 = 1.521.
Sisi-sisi lainnya memiliki panjang 15 cm dan 36 cm. Kamu dapatkan 152 = 225 dan 362 = 1.296.
Coba perhatikan bahwa 152 + 362 = 225 + 1.296 = 1.521.
Jadi, 152 + 362 = 392 .
Oleh karena pada ∆ABC sisi-sisinya memenuhi teorema Pythagoras, maka ∆ABC merupakan segitiga siku-siku.
S1
Pilihan Tunggal
Jika panjang salah satu sisi segitiga siku-siku adalah 15 cm dan panjang sisi miringnya 17 cm, maka panjang sisi lainnya adalah ….
S2
Pilihan Tunggal
Nilai x pada bangun berikut ini adalah ….

S3
Pilihan Tunggal
∆GHI dengan panjang sisi 6 cm, 5 cm, dan 3 cm merupakan segitiga ….
S4
Pilihan Tunggal
∆DEF dengan panjang sisi 8 cm, 9 cm, dan 6 cm merupakan segitiga ….
S5
Pilihan Tunggal
Diketahui ∆ABC siku-siku di A. Panjang sisi miring BC = 20 cm. Jika perbandingan panjang kedua sisi siku-sikunya 3 : 4, maka luas segitiga tersebut adalah … cm2 .
S6
Pilihan Tunggal
Kelompok bilangan yang merupakan tripel Pythagoras adalah ….
S7
Pilihan Tunggal
Diketahui sebuah ∆ABC. Jika panjang sisi AB = 18 cm, AC = 30 cm, dan BC = 24 cm, maka pernyataan yang benar adalah ….
S8
Pilihan Tunggal
Diketahui sisi-sisi segitiga adalah sebagai berikut.
(1). 5n, 12n, dan 13n, dengan n bilangan asli
(2). (n + 3), (n + 4), dan (n + 5), dengan n bilangan asli
(3). 7n, 24n, dan 25n, dengan n bilangan asli
Sisi-sisi yang membentuk segitiga siku-siku adalah ….
S9
Pilihan Tunggal
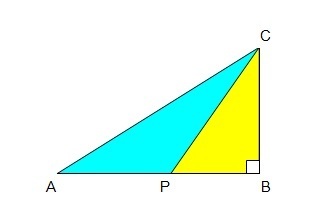
Pada gambar berikut ini, diketahui ∆ABC siku-siku di B. Titik P membagi sisi AB menjadi dua bagian sama panjang. Jika panjang BC = 3 cm dan PC = 4 cm, maka perbandingan luas ∆PBC dengan luas ∆APC adalah ….

S10
Pilihan Tunggal
Perhatikan gambar bangun berikut.

Jika panjang AC = 9, maka AD = ….

Tidak ada komentar:
Posting Komentar