Contoh Soal Menggambar Grafik Fungsi Kuadrat - Pernahkah kamu bermain bola basket? Saat kamu melakukan shooting, bola akan melambung menuju keranjang atau ring basket, seperti gambar di bawah ini.


Tentang:
Matematika

Sumber gambar: http://id.wikipedia.org/wiki/Bola_basket
Pelemparan bola dapat digambarkan seperti grafik berikut.

Grafik pelemparan bola yang menyerupai parabola tersebut merupakan salah satu contoh grafik fungsi kuadrat. Grafik fungsi menunjukkan pemetaan atau fungsi dari suatu himpunan ke himpunan lainnya. Grafik fungsi dibentuk dalam suatu diagram Cartesius. Agar kamu lebih paham tentang cara menggambar grafik fungsi kuadrat, mari kita ingat kembali tentang pengertian fungsi.
Pengertian Fungsi
Fungsi (pemetaan) dari himpunan A ke himpunan B adalah relasi khusus yang memasangkan setiap anggota A dengan tepat satu anggota himpunan B.
Pengertian Fungsi Kuadrat
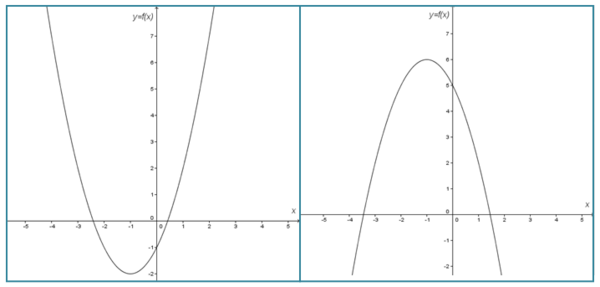
Fungsi kuadrat merupakan fungsi dengan pangkat terbesar dari variabel bebas (misalnya variabel x) adalah dua dan bentuk umumnya f (x) = y = ax2 + bx + c. Bentuk grafik fungsi kuadrat menyerupai parabola.
Contoh grafik fungsi kuadrat yaitu:

Menggambar Grafik Fungsi Kuadrat
Langkah-langkah menggambar grafik fungsi kuadrat adalah sebagai berikut.
- Tentukan titik potong terhadap sumbu x dengan syarat y = 0, sehingga diperoleh koordinat (x1 , 0) dan (x2 , 0).
- Tentukan titik potong terhadap sumbu y dengan syarat x = 0, sehingga diperoleh koordinat (0, y1).
- Tentukan titik balik atau titik puncak .
- Gambarkan dan hubungkan titik-titik yang diperoleh pada bidang Cartesius.
✎Contoh 1
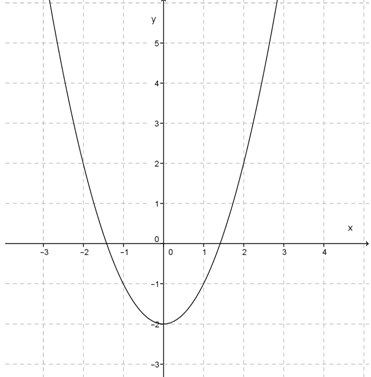
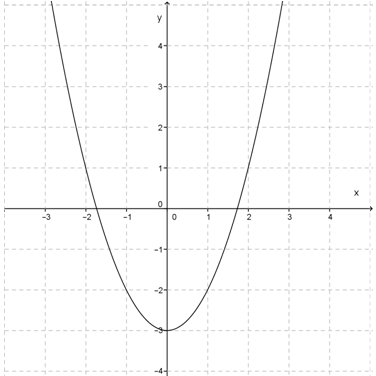
Gambarkan grafik fungsi y = x2 – 1.
Penyelesaian:
Diketahui fungsi y = x2 – 1 dengan a = 1, b = 0, c = -1.
- Titik potong sumbu x dengan syarat y = 0.
y = x2 – 1
⇔ 0 = x2 – 1
⇔ (x + 1) (x - 1) = 0
⇔ x = -1 atau x = 1
⇔ 0 = x2 – 1
⇔ (x + 1) (x - 1) = 0
⇔ x = -1 atau x = 1
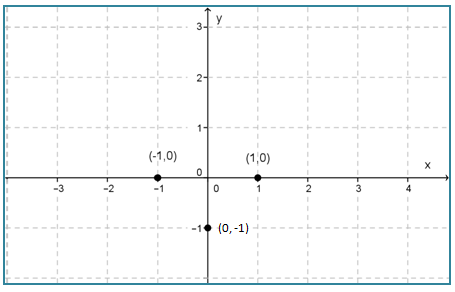
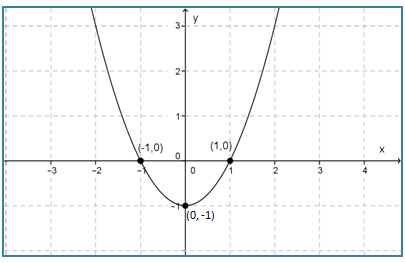
∴ Titik potong sumbu x adalah (-1, 0) dan (1, 0).

- Titik potong sumbu y dengan syarat x = 0.
y = x2 – 1
⇔ y = 0 – 1
⇔ y = -1
⇔ y = 0 – 1
⇔ y = -1
∴ Titik potong sumbu y adalah (0, -1).

- Titik balik
∴ Titik baliknya adalah (0, -1)
Ini berarti, titik baliknya sama dengan titik potong fungsi dengan sumbu y.
- Hubungkan titik-titik yang diperoleh pada bidang Cartesius, sehingga terbentuk grafik y = x2 – 1 seperti di bawah ini.

✎Contoh 2
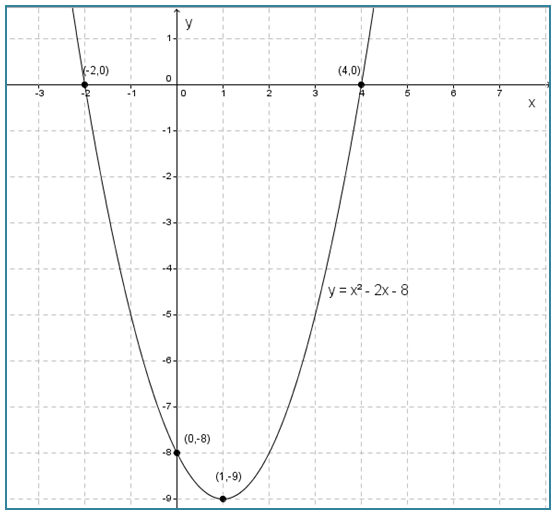
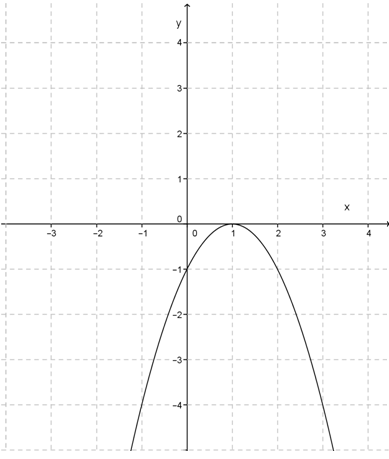
Gambarkan grafik fungsi y = x2 – 2x - 8.
Penyelesaian:
Diketahui fungsi y = x2 – 2x - 8 dengan a = 1, b = -2, dan c = -8.
- Titik potong sumbu x dengan syarat y = 0.
y = x2 – 2x - 8
⇔ 0 = x2 – 2x - 8
⇔ (x - 4) (x + 2) = 0
⇔ x = 4 atau x = -2.
⇔ 0 = x2 – 2x - 8
⇔ (x - 4) (x + 2) = 0
⇔ x = 4 atau x = -2.
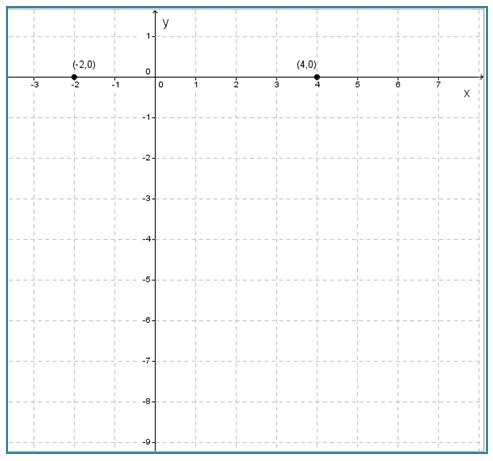
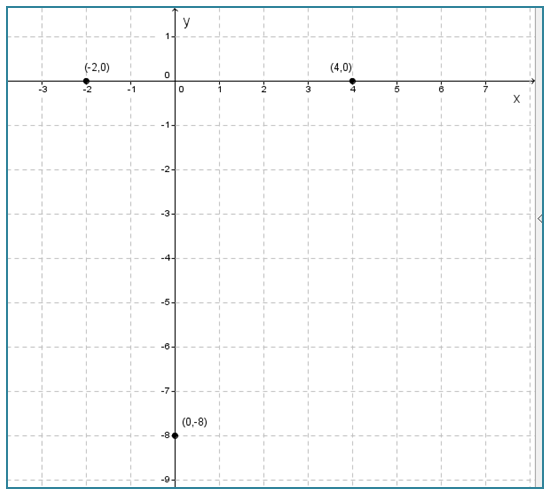
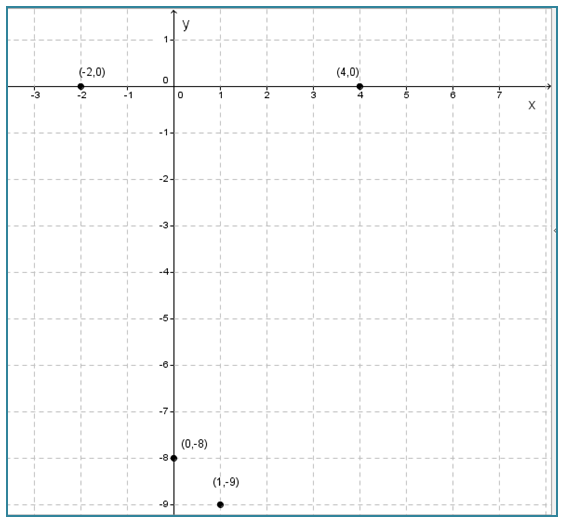
∴ Titik potong sumbu x adalah (-2, 0) dan (4, 0).

- Titik potong sumbu y dengan syarat x = 0.
y = x2 – 2x - 8
⇔ y = 0 – 0 – 8
⇔ y = -8
⇔ y = 0 – 0 – 8
⇔ y = -8
∴ Titik potong sumbu y adalah (0, -8).

- Titik balik
∴ Titik baliknya adalah (1, -9).

- Hubungkan titik-titik yang diperoleh pada bidang Cartesius, sehingga terbentuk grafik y = x2 – 2x - 8 seperti di bawah ini.

✎Contoh 3
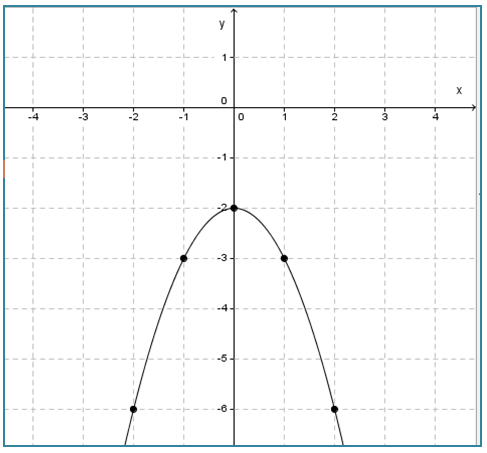
Gambarkan grafik fungsi f : x → -x2 – 2 dengan domain adalah {-2, -1, 0, 1, 2} dan rangenya adalah himpunan bilangan real.
Penyelesaian :
Diketahui:
f (x) = -x2 – 2
domain f (x) = {-2, -1, 0, 1, 2}
Diketahui:
f (x) = -x2 – 2
domain f (x) = {-2, -1, 0, 1, 2}
Range (daerah hasil) dari f (x) dapat ditentukan dengan mensubstitusikan anggota domain ke f (x).
f (x) = -x2 – 2
f (-2) = -(-2)2 – 2 = -6
f (-1) = -(-1)2 – 2 = -3
f (0) = -(0)2 – 2 = -2
f (1) = -(1)2 – 2 = -3
f (2) = -(2)2 – 2 = -6
f (-2) = -(-2)2 – 2 = -6
f (-1) = -(-1)2 – 2 = -3
f (0) = -(0)2 – 2 = -2
f (1) = -(1)2 – 2 = -3
f (2) = -(2)2 – 2 = -6
Pasangan berurutan dari domain dan range f (x) adalah:
(-2, -6), (-1, -3), (0, -2), (1, -3), (2, -6)
(-2, -6), (-1, -3), (0, -2), (1, -3), (2, -6)
Gambarkan pasangan berurutan tersebut dalam bentuk titik (noktah) pada bidang Cartesius kemudian hubungkan, sehingga membentuk grafik y = x2 – 2x - 8 seperti di bawah ini.

S1
Pilihan Tunggal
Grafik yang merupakan grafik fungsi kuadrat adalah ....
S2
Pilihan Tunggal
Jika y = x2 – 5x + 6, maka koordinat titik balik dari fungsi tersebut adalah ....
S3
Pilihan Tunggal
Diketahui grafik fungsi berikut.

Jika y = {1, 4}, maka x = ....
S4
Pilihan Tunggal
Diketahui gambar berikut.

Jika x = {x | 0 ≤ x < 3, x ϵ bilangan bulat}, maka y = ....
S5
Pilihan Tunggal
Grafik dari fungsi kuadrat y = x2 – 4 adalah ....
S6
Pilihan Tunggal
Grafik dari fungsi kuadrat y = x2 – 4x + 3 adalah ....
S7
Pilihan Tunggal
Grafik dari fungsi kuadrat y = -x2 + 1 adalah ....
S8
Pilihan Tunggal
Perhatikan pernyataan-pernyataan berikut.
(1) Jika x = 0, maka y = 3
(2) Jika x = 0, maka y = -3
(3) Grafik fungsi

(4) Grafik fungsi

Jika diketahui y = x2 – 3, maka pernyataan yang benar adalah ....
S9
Pilihan Tunggal
Perhatikan pernyataan-pernyataan berikut.
(1) Jika y = 0, maka x = 1
(2) Jika y = 0, maka x = -2 atau x = 2
(3) Grafik fungsi

(4) Grafik fungsi

Jika diketahui y = -x2 + 2x - 1, maka pernyataan yang benar adalah ....
S10
Pilihan Tunggal
Perhatikan pernyataan-pernyataan berikut.
(1) Jika x = 0, maka y = 4
(2) Jika y = 0, maka x = -2 atau x = 2
(3) Grafik fungsi

(4) Grafik fungsi

Jika diketahui y = -x2 + 4, maka pernyataan yang benar adalah ....

Tidak ada komentar:
Posting Komentar