Contoh Soal Menyelesaikan SPLDV dengan Metode Grafik - Pada kedua topik sebelumnya kamu telah mempelajari tentang pengertian sistem persamaan linear dua variabel. Apakah kamu tahu kegunaan dari sistem persamaan linear dalam kehidupan nyata? Dalam kehidupan nyata, sistem persamaan linear sering ditemui dalam industri seperti pada perhitungan hasil maksimal dari sebuah produksi pangan atau komoditas lain.

Tentang:
Matematika

Sumber gambar: flickr.com
Saat ini, kamu akan mempelajari sistem persamaan linear dua variabel, tetapi pada tingkatan selanjutnya kamu akan mempelajari sistem persamaan linear lebih dari dua variabel. Ada beberapa cara untuk menyelesaikan sistem persamaan linear dua variabel, yaitu:
- metode grafik.
- metode substitusi.
- metode elminasi.
Pada topik kali ini, kamu akan mempelajari tentang cara menyelesaikan SPLDV dengan metode grafik. Masih ingatkah kamu dengan cara menggambar grafik sebuah persamaan dua variabel atau persamaan garis? Mari simak contohnya berikut ini.
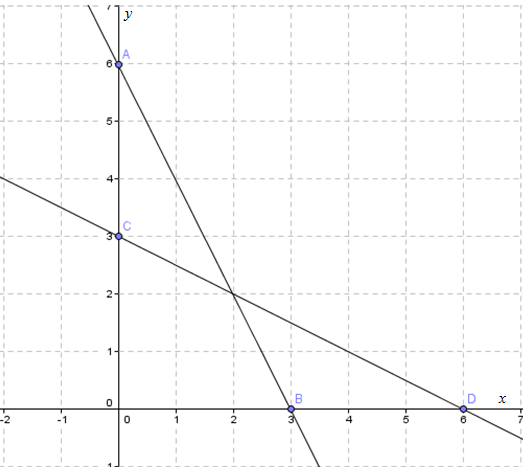
✎Contoh 1
Gambarkan grafik untuk persamaan 2x + y = 4.
Penyelesaian:
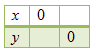
Untuk menggambarkan grafik SPLDV, gunakan paling sedikit dua titik seperti pada tabel berikut.

Tentukan nilai y untuk x = 0.
2x + y = 4
⇔2( 0) + y = 4
⇔y = 4
2x + y = 4
⇔2( 0) + y = 4
⇔y = 4
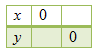
Tentukan nilai x untuk y = 0.
2x + y = 4
⇔ 2x + 0 = 4
⇔ 2x = 4
⇔ x = 2
2x + y = 4
⇔ 2x + 0 = 4
⇔ 2x = 4
⇔ x = 2
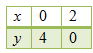
Tuliskan hasil yang diperoleh ke dalam tabel.

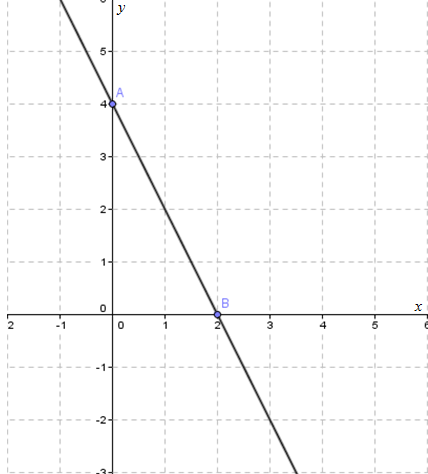
Ini berarti, titik yang diperoleh adalah A (0, 4) dan B (2, 0).
Gambarkan titik tersebut ke dalam diagram Cartesius, kemudian hubungkan dengan sebuah garis lurus, sehingga terbentuk gambar di bawah ini.

Langkah-langkah menyelesaikan SPLDV dengan metode grafik adalah sebagai berikut.
- Gambarkan grafik untuk persamaan pertama.
- Gambarkan grafik untuk persamaan kedua.
- Tentukan perpotongan dua grafik tersebut yang merupakan penyelesaian dari SPLDV.
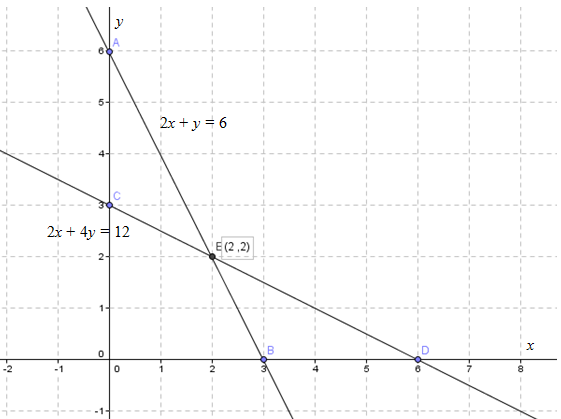
✎Contoh 2
Tentukan penyeselesaian dari SPLDV:
2x + y = 6
2x + 4y = 12
2x + y = 6
2x + 4y = 12
Penyelesaian:
Langkah 1: gambarkan grafik untuk persamaan pertama.
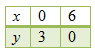
Gunakan paling sedikit dua titik seperti pada tabel berikut.

Tentukan nilai y untuk x = 0.
2x + y = 6
⇔ 2(0) + y = 6
⇔ y = 6
2x + y = 6
⇔ 2(0) + y = 6
⇔ y = 6
Tentukan nilai x untuk y = 0.
2x + y = 6
⇔2x + 0 = 6
⇔2x = 6
⇔x = 3
2x + y = 6
⇔2x + 0 = 6
⇔2x = 6
⇔x = 3
Tuliskan hasil yang diperoleh ke dalam tabel.

Ini berarti, titik yang diperoleh adalah A (0, 6) dan B (3, 0).
Gambarkan titik tersebut ke dalam diagram Cartesius, kemudian hubungkan dengan sebuah garis lurus, sehingga terbentuk gambar di bawah ini.

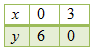
Langkah 2: gambarkan grafik untuk persamaan kedua.
Gunakan paling sedikit dua titik seperti pada tabel berikut.

Tentukan nilai y untuk x = 0.
2x + 4y = 12
⇔ 0 + 4y = 12
⇔ 4y = 12
⇔ y = 3
2x + 4y = 12
⇔ 0 + 4y = 12
⇔ 4y = 12
⇔ y = 3
Tentukan nilai x untuk y = 0.
2x + 4y = 12
⇔ 2x + 4.0 = 12
⇔ 2x = 12
⇔ x = 6
2x + 4y = 12
⇔ 2x + 4.0 = 12
⇔ 2x = 12
⇔ x = 6
Tuliskan hasil yang diperoleh ke dalam tabel.

Ini berarti, titik yang diperoleh adalah C (0, 3) dan D (6, 0).
Gambarkan titik tersebut ke dalam diagram Cartesius, kemudian hubungkan dengan sebuah garis lurus, sehingga terbentuk gambar di bawah ini.

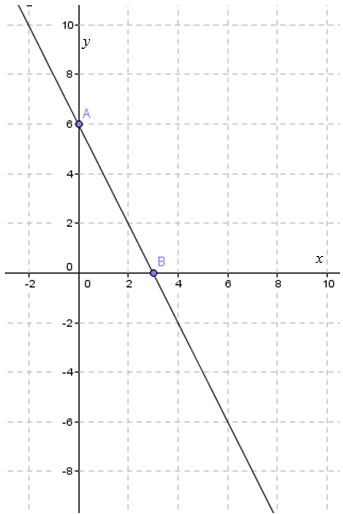
Langkah 3: Tentukan perpotongan dua grafik (garis) yang merupakan penyelesaian dari SPLDV.
Perhatikan gambar berikut.

Berdasarkan gambar di atas, titik potong kedua grafik adalah pada koordinat (2,2).
Jadi, penyelesaian dari SPLDV tersebut adalah (2, 2).
S1
Pilihan Tunggal
Penyelesaian dari SPLDV dengan grafik di bawah ini adalah ...

S2
Pilihan Tunggal
Perhatikan grafik berikut.

Penyelesaian dari SPLDV pada gambar adalah ....
S3
Pilihan Tunggal
Penyelesian dari SPLDV 2x – 3y = 6 dan 2x + 3y = 18 adalah ....
S4
Pilihan Tunggal
Penyelesaian dari sistem persamaan 3x - 5y = 15 dan -3x - y = 3 adalah ....
S5
Pilihan Tunggal
Penyelesaian dari SPLDV 2x + 5y + 10 = 0 dan -4x + y + 24 = 0 adalah ….
S6
Pilihan Tunggal
Diketahui SPLDV 4x – y = -2 dan x + y = -3. Nilai dari 2x + 3y = ….
S7
Pilihan Tunggal
Jika penyelesaian dari SPLDV dengan salah satu persamaan linearnya 3x – 2y = 12 adalah (4, 0), maka persamaan linear yang lain adalah ....
S8
Pilihan Tunggal
SPLDV yang mempunyai penyelesaian (2 , 1) adalah ....
S9
Pilihan Tunggal
SPLDV yang memiliki penyelesaian tunggal adalah ….
S10
Pilihan Tunggal
Suatu bilangan x tiga lebihnya dari bilangan y. Jika jumlah kedua bilangan adalah 13, maka x adalah ….

Tidak ada komentar:
Posting Komentar