Contoh Soal Pengertian Sistem Persamaan Linear Dua Variabel (SPLDV)

Contoh Soal Pengertian Sistem Persamaan Linear Dua Variabel (SPLDV) - Pada topik ini, kita akan mempelajari tentang Sistem Persamaan Linear Dua Variabel (SPLDV) yang merupakan topik lanjutan dari Persamaan Linear Dua Variabel (PLDV). SPLDV merupakan gabungan dari dua atau lebih PLDV yang sudah dipelajari sebelumya. Oleh karena SPLDV banyak diterapkan dalam kehidupan sehari-hari, maka pelajarilah dengan saksama uraiannya berikut ini.

Mari simak ilustrasi berikut.

       Dalam sebuah gedung bioskop berkapasitas 200 orang, dijual tiket yang terdiri dari dua kelas yaitu kelas VIP dengan harga Rp20.000,00 dan kelas ekonomi Rp10.000,00. Pada saat pertunjukan, gedung bioskop penuh penonton dan diperoleh pemasukan tiket Rp2.800.000,00. Berapakah banyak penonton kelas VIP dan kelas ekonomi?

       Kasus di atas dapat diselesaikan dengan menggunakan SPLDV. Misalkan x adalah banyak penonton kelas VIP dan y adalah banyak penonton kelas ekonomi. Persamaan linear untuk banyak penonton dari setiap kelas dan pemasukan tiket (dalam rupiah) adalah:

x + y = 200
dan 
20.000x + 10.000y = 2.800.000

Untuk menentukan nilai x dan y diperlukan metode yang akan dibahas pada topik selanjutnya.

Perhatikan masalah lainnya di bawah ini.

       Ibu Ani dan ibu Budi pergi berbelanja ke pasar. Ibu Ani membeli 3 kg semangka dan 4 kg melon dengan harga Rp5.800,00. Ibu Budi membeli 4 kg semangka dan 3 kg melon dengan harga Rp6.100,00. Bagaimanakah bentuk sistem persamaan linear dua variabel dari kasus tersebut?

Kasus di atas dapat diselesaikan dengan memisalkan s sebagai harga 1 kg semangka dan m sebagai harga 1 kg melon. Ini berarti, pembelian ibu Ani dapat dimisalkan dengan:
3s + 4m = 5.800
pembelian ibu Budi dapat dimisalkan dengan:
4s + 3m = 6.100

Dengan demikian, diperoleh sistem persamaan linear dua variabel dari kasus tersebut adalah:

$\{\begin{array}{l}3s+4m=5.800\\ 4s+3m=6.100\end{array}$

Sistem Persamaan Linear Dua Variabel (SPLDV) terdiri dari dua buah atau lebih persamaan linear dua variabel. Bentuk umum SPLDV adalah:

$\{\begin{array}{l}ax+by=c\\ px+qy=r\end{array}$

dengan x dan y adalah variabel, a, p, b, dan q adalah koefisien dari x dan y, serta c, r adalah konstanta.

Ciri-ciri SPLDV adalah sebagai berikut .

• Terdiri dari dua atau lebih Persamaan Linear Dua Variabel (PLDV) yaitu persamaan yang terdiri dari dua variabel yang berpangkat tertinggi satu.
• Tidak terdapat perkalian variabel dalam setiap persamaannya.
• PLDV yang ada dalam SPLDV terdiri dari dua macam variabel yang sama.

✎Contoh 1

Identifikasi bentuk yang termasuk SPLDV dari sistem persamaan berikut.

• $\{\begin{array}{l}5x+y=6\\ x+7y=5\end{array}$

Penyelesaian:

5x + 6y = 6 merupakan persamaan linear dua variabel karena terdiri dari dua variabel dengan pangkat tertinggi satu.

x + 7y = 5 merupakan persamaan linear dua variabel karena terdiri dari dua variabel dengan pangkat tertinggi satu.

$\{\begin{array}{l}5x+y=6\\ x+7y=5\end{array}$ merupakan SPLDV karena kedua PLDV-nya memiliki dua macam variabel yang sama yaitu x dan y.

Nilai a, b, c, p, q, r dari SPLDV tersebut berturut-turut adalah 5, 1, 6, 1, 7, 5.

• $\{\begin{array}{l}2xy+y=6\\ 3x+2y=9\end{array}$

Penyelesaian:

2xy + y = 6 bukan merupakan persamaan linear karena memuat perkalian dua variabel yaitu xy.

Oleh karena SPLDV harus terdiri dari persamaan linear, maka sistem persamaan tersebut bukanlah SPLDV.

Sebelum mempelajari metode khusus untuk menentukan penyelesaian (solusi) SPLDV pada topik-topik berikutnya, kamu dapat menggunakan teknik coba-coba seperti yang dijelaskan pada contoh di bawah ini.

✎Contoh 2

Tentukan penyelesaian dari SPLDV:

$\{\begin{array}{l}2x+y=9\\ 4x-y=3\end{array}$

Penyelesaian:

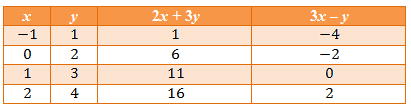
Kita dapat menggunakan teknik coba-coba yaitu dengan menerka-nerka pasangan bilangan x dan y yang memenuhi penyelesaian SPLDV yang diketahui melalui tabel berikut.

Perhatikan bahwa untuk nilai x = 2 dan y = 5 masing-masing memenuhi 2x + y = 9 dan 4x - y = 3.

Jadi, penyelesaian dari SPLDV di atas adalah x = 2 dan y = 5.

Pada topik-topik selanjutnya, akan dibahas cara menentukan penyelesaian SPLDV dengan menggunakan:

• metode grafik
• metode subsitusi
• metode eliminasi
• metode campuran

S1

Pilihan Tunggal

Koefisien y dari sistem persamaan linier $\{\begin{array}{l}2y+3x=7\\ x+9y=3\end{array}$ adalah ....

S2

Pilihan Tunggal

Dari beberapa persamaan berikut, yang merupakan sistem persamaan linear dua variabel adalah ....

S3

Pilihan Tunggal

Dari beberapa persamaan berikut yang merupakan sistem persamaan linear dua variabel adalah ....

S4

Pilihan Tunggal

Tabel berikut merupakan hasil teknik coba-coba untuk menentukan nilai x dan y yang memenuhi dari $\{\begin{array}{l}2x+3y=6\\ 3x-y=-2\end{array}$.

Berdasarkan tabel tersebut, penyelesaian dari SPLDV diatas adalah ....

S5

Pilihan Tunggal

Diketahui sistem persamaan $\{\begin{array}{l}\frac{1}{a}+\frac{3}{b}=7\\ \frac{5}{a}+\frac{7}{b}=3\end{array}$. Jika pada sistem persamaan itu dilakukan pergantian setiap $x=\frac{1}{a}\mathrm{d}\mathrm{a}\mathrm{n}y=\frac{1}{b}$, maka sistem persamaan linear yang terbentuk adalah ....

S6

Pilihan Tunggal

Jumlah dua bilangan cacah adalah 27 dan selisih kedua bilangan itu adalah 3. Sistem persamaan linear dari pernyataan tersebut jika bilangan pertama adalah x dan bilangan kedua adalah y yaitu ....

S7

Pilihan Tunggal

Dua kali jumlah dua bilangan bulat positif adalah 58 dan selisih kedua bilangan itu adalah 7. Bentuk SPLDV dari pernyataan tersebut jika bilangan pertama adalah x dan bilangan kedua adalah y adalah ....

S8

Pilihan Tunggal

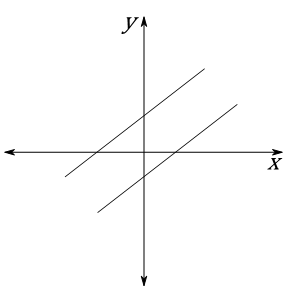
Perhatikan diagram Cartesius berikut berikut.

Jika kedua garis sejajar, maka pilihan sistem persamaan linear yang mungkin untuk mewakili persamaan-persamaan garis tersebut adalah ....

S9

Pilihan Tunggal

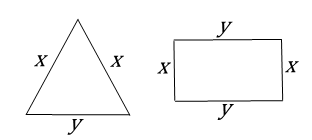
Perhatikan gambar dua bangun datar di bawah ini.

Jika keliling segitiga dan persegipanjang di atas adalah 16 satuan dan 25 satuan, maka sistem persamaan linear yang mewakili keliling kedua bangun tersebut adalah ....

S10

Pilihan Tunggal

Persamaan garis yang melalui titik (2, -3) dan tegak lurus dengan garis x + y = 10 adalah ....

Tentang: Matematika

Share:

Artikel Terkait