Contoh Soal Persamaan Linear Dua Variabel

Contoh Soal Persamaan Linear Dua Variabel - Kalian tentu sudah memahami tentang persamaan linear satu variabel bukan? Lantas, bagaimana jika persamaan tersebut melibatkan dua variabel? Pada topik ini, kalian akan mempelajarinya. Persamaan linear dua variabel yang akan kalian pelajari ini, akan sangat membantu kalian untuk mempelajari topik selanjutnya, yaitu Sistem Persamaan Linear Dua Variabel (SPLDV). Topik ini merupakan kasus umum dari persamaan garis lurus yang sudah pernah kamu pelajari di topik sebelumnya. Mari pelajari dan pahami dengan baik topik ini.

PENDAHULUAN

Di sebuah desa, terdapat sepasang manula yang tinggal di rumah tua. Pada saat sensus penduduk tahun 2014, kakek dan nenek tersebut belum memiliki KTP, kakek dan nenek diminta data tahun lahirnya. Mereka hanya mengingat bahwa selisih umur mereka adalah 3 tahun dan kakek lebih tua dari nenek. Setelah diteliti, ternyata kakek lahir saat Indonesia meraih kemerdekaan. Dapatkah kamu membuat persamaan linear dari persoalan di atas? Dapatkah kamu mengetahui tahun lahir mereka?

          Kasus di atas dapat diselesaikan dengan menggunakan persamaan linear dua variabel. Misalkan tahun lahir kakek adalah Kdan tahun lahir nenek adalah N. Oleh karena selisih umur mereka adalah 3 tahun dan kakek lebih tua dari nenek, maka diperoleh persamaan linear dua variabel:

                                                                         N - K = 3

          Agar kalian lebih memahami tentang persamaan linear dua variabel dan cara menyelesaikannya, simak topik ini dengan saksama ya.

Kalian pasti sudah mempunyai sedikit bayangan tentang perngertian persamaan linear dua variabel ini. Agar lebih jelas lagi, perhatikan beberapa contoh persamaan linear dua variabel berikut ini.

• 2x + y = 3
• 2a - b = 17
• m + n = 12
• 4a + 3b = a + 7
• x + y + 7 = 9
• r - 2q = 23

          Persamaan-persamaan tersebut memuat dua variabel yang belum diketahui nilainya. Persamaan-persamaan seperti itulah yang dimaksud dengan persamaan linear dua variabel. Kamu pasti merasa bahwa persamaan-persamaan di atas sama seperti persamaan garis lurus yang sudah pernah kamu pelajari sebelumnya. Ya, persamaan garis lurus merupakan salah satu contoh persamaan linear dua variabel.

          Persamaan linear dua variabel adalah persamaan linear yang hanya memiliki dua variabel, dengan pangkat masing-masing variabel adalah satu. Dalam persamaan linear dua variabel, tidak ada perpangkatan dalam variabelnya atau perkalian antarvariabelnya. Persamaan linear dua variabel memiliki bentuk umum :

                                                                         ax + by = c

dengan a, b, dan c adalah konstanta real; x dan y adalah variabel.

►  Contoh 1

Dari persamaan berikut ini, tentukan yang termasuk persamaan linear dua variabel dan yang bukan.

a. x + 3y = 2

b. x2 + y = 1

c. a - b - 2 = 2

Penyelesaian:

a. Persamaan linear dua variabel adalah persamaan linear yang hanya memiliki dua variabel, dengan pangkat masing-masing variabel adalah satu.

Oleh karena x + 3y = 2 memiliki dua variabel, yaitu x dan y, serta pangkat masing-masing variabel satu, maka x + 3y = 2 merupakan persamaan linear dua variabel.

b. Persamaan linear dua variabel adalah persamaan linear yang hanya memiliki dua variabel, dengan pangkat masing-masing variabel adalah satu.

x2 + y = 1 memiliki 2 variabel, yaitu x dan y, akan tetapi pangkat salah satu variabelnya bernilai 2, sehingga x2 + y = 1 bukan persamaan linear dua variabel.

c. Persamaan linear dua variabel adalah persamaan linear yang hanya memiliki dua variabel, dengan pangkat masing-masing variabel adalah satu.

Oleh karena a - b - 2 = 2 memiliki dua variabel, yaitu a dan b, serta pangkat masing-masing variabel satu, maka a - b - 2 = 2 merupakan persamaan linear dua variabel. a - b - 2 = 2 juga dapat dinyatakan dengan a - b = 4.

          Lantas, bagaimana cara menentukan penyelesaian dan himpunan penyelesaian persamaan linear dua variabel? Penyelesaian persamaan linear dua variabel dapat ditentukan dengan mensubsitusikan nilai yang sesuai untuk kedua variabelnya hingga memenuhi persamaan tersebut. Bentuk penyelesaiannya berupa koordinat dari kedua variabel tersebut, misalnya (x, y) dan himpunan penyelesaiannya berupa {(x, y)}. Untuk memahaminya, perhatikan contoh berikut.

►  Contoh 2

Tentukan himpunan penyelesaian dari persamaan linear dua variabel 2m + n = 4, dengan m, n ∈ cacah.

Penyelesaian:

Diketahui 2m + n = 4, dengan m, n ∈ cacah.

Jika m = 0, maka:

2m + n = 4

⇔2(0) + n = 4

⇔n = 4

Diperoleh m = 0 dan n = 4, dapat dituliskan dengan (0, 4).

Jika m = 1, maka:

2m + n = 4

⇔2(1) + n = 4

⇔n = 2

Diperoleh m = 1 dan n = 2, dapat dituliskan dengan (1, 2).

Jika m = 2, maka:

2m + n = 4

⇔2(2) + n = 4

⇔n = 0

Diperoleh m = 2 dan n = 0, dapat dituliskan dengan (2, 0).

Jika m = 3, maka:

2m + n = 4

⇔2(3) + n = 4

⇔n = -2

Diperoleh m = 3 dan n = -2. Nilai n = -2 tidak memenuhi syarat karena bukan anggota bilangan cacah.

Jadi, himpunan penyelesaian dari 2m + n = 4 dengan m, n ∈ cacah adalah {(0, 4)(1, 2)(2, 0)}.

Sekarang, mari kita kembali pada ilustrasi di atas. Kita akan tentukan penyelesaian dari persamaan linear yang terbentuk.

Oleh karena kakek lahir saat Indonesia meraih kemerdekaan, yaitu pada tahun 1945, maka K = 1945. Subsitusikan nilai K ini ke persamaan linear dua variabel diperoleh, sehingga:

N - K = 3

⇔N - 1945 = 3

⇔N = 1945 + 3

⇔N = 1948

Jadi, tahun lahir kakek dan nenek masing-masing adalah 1945 dan 1948.

Agar kalian lebih paham lagi, perhatikan contoh kasus lain persamaan linear dua variabel berikut ini.

►  Contoh 3

Umur Susi sekarang adalah 13 tahun. Lima tahun yang akan datang, umur Yanti sama dengan 2 kali umur Susi. Berapakah umur Yanti sekarang?

Penyelesaian:

Kasus di atas juga dapat diselesaikan dengan menggunakan persamaan linear dua variabel. Misalkan umur Susi adalah S dan umur Yanti adalah Y.

Oleh karena lima tahun yang akan datang umur Yanti sama dengan 2 kali umur Susi, maka persamaan linear dua variabel yang terbentuk adalah:

Y + 5 = 2(S + 5)

⇔Y + 5 = 2S + 10

⇔Y = 2S + 5

⇔Y - 2S = 5.

Oleh karena umur Susi sekarang adalah 13 tahun, maka S = 13. Dengan demikian, umur Yanti dapat diperoleh dengan mensubsitusikan nilai S ke persamaan di atas, sehingga diperoleh:

Y - 2S = 5

⇔Y - 2(13) = 5

⇔Y - 26 = 5

⇔Y = 31

Jadi, umur Yanti sekarang adalah 31 tahun.

S1

Pilihan Tunggal

Dari beberapa persamaan berikut, yang merupakan persamaan linear dua variabel adalah ....

S2

Pilihan Tunggal

Salah satu anggota himpuan penyelesaian dari 5x + y = 14 adalah ....

S3

Pilihan Tunggal

Berikut ini yang bukan merupakan anggota himpunan penyelesaian dari 3x + y = 12 adalah ....

S4

Pilihan Tunggal

Jika diketahui $\frac{x}{3}-\frac{y}{5}=1$ memenuhi bentuk ax + by = c , maka nilai a, b, dan c adalah ....

S5

Pilihan Tunggal

Apabila persamaan linear dua variabel 2y - 3x = 7 dinyatakan dalam bentuk persamaan garis lurus y = mx + c, maka variabel x akan memiliki koefisien sebesar ....

S6

Pilihan Tunggal

Diketahui suatu garis lurus memiliki titik-titik ujung (0, 6) dan (6, 0). Persamaan linear dua variabel yang mewakili garis tersebut adalah ....

S7

Pilihan Tunggal

Jika persamaan garis lurus di bawah ini dinyatakan dalam dalam bentuk umum persamaan linear dua variabel, maka koefisien y dari persamaan tersebut adalah ....

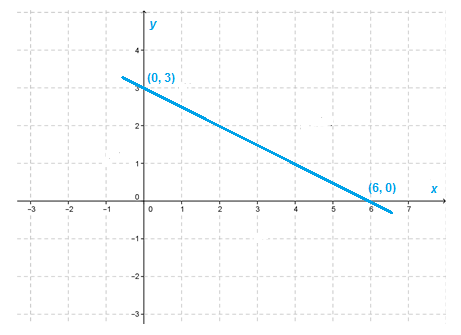
S8

Pilihan Tunggal

Diketahui keliling sebuah segitiga samakaki adalah 44 cm. Jika panjang sisi segitiga yang sama panjang adalah y dan panjang sisi lainnya adalah x , persamaan linear dua variabel yang mewakili keliling tersebut adalah ....

S9

Pilihan Tunggal

Diketahui keliling sebuah persegipanjang adalah 84 cm. Jika panjang sisi persegipanjang adalah x dan panjang sisi lebarnya adalah y, persamaan linear dua variabel yang mewakili keliling tersebut adalah....

S10

Pilihan Tunggal

Nelly mempunyai uang sebesar Rp57.500,00, sedangkan uang Lina sebesar Rp6.250,00 lebih banyak dari uang Nelly. Jumlah uang Lina adalah ....

Tentang: Matematika

Share:

Artikel Terkait