Contoh Soal Grafik polinomial - Ada dua aspek penting dari polinomial untuk membuat grafik sebuah fungsi, yaitu: kelakuan (behavior) dan akar.
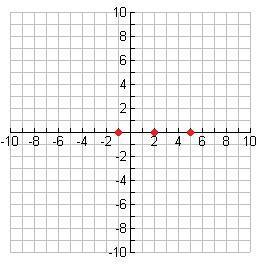
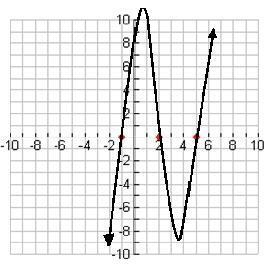
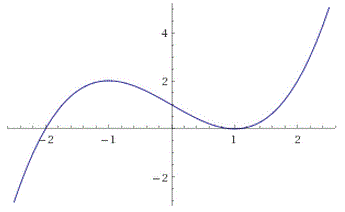
f(x) = x 4 + x 3- 2x 2
Tentang:
MIA kelas 11
Akar-akar dari sebuah Polinomial
Akar-akar dari sebuah fungsi polinomial adalah titik pada grafik dimana fungsi tersebut berpotongan dengan sumbu-X atau dimana fungsi tersebut sama dengan nol. Cara yang paling mudah untuk menemukan nol dari polinomial adalah memfaktorkan fungsinya. Sebuah polinomial dalam bentuk pemfaktoran, seperti (x+1) (x-2), akan memiliki akar x=-1 dan x=2. Namun, polinomial paling sering terdapat dalam bentuk non faktor , seperti x2-3x-4, yang difaktorkan menjadi (x-4) (x+1). Tidak ada metode khusus untuk pemfaktoran, tapi lebih kepada elemen untuk “melihatnya.” Cara terbaik untuk mudah mengenali faktor-faktor tersebut adalah dengan latihan. Mari kita coba contoh berikut ini:
Faktorkan: 3x2-24x-27
Langkah Pertama: Faktorkan keluar 3, yang menghasilkan 3(x2-8x-9)
Langkah Kedua: Sekarang polinomialnya berada dalam bentuk yang jauh lebih mudah untuk difaktorkan, dan kita dapat menulis ulang polinomialnya menjadi 3(x-9)(x+1)
Kelakuan (Behavior)
Elemen penting kedua adalah kelakuan (behavior) fungsi. Kelakuan (Behavior) menjelaskan bagaimana fungsi bertindak pada titik-titik kunci, khususnya ketika x mendekati ±∞. Jika sebuah fungsi dinaikkan pada sebuah eksponen genap (x2 atau x4) dan memiliki sebuah koefisien utama positif ketika x mendekati ±∞ fungsinya akan menjadi +∞. Jika sebuah fungsi dengan sebuah eksponen genap dan memiliki koefisien utama negatif ketika x mendekati ±∞ fungsinya akan menjadi -∞. Tapi jika fungsinya dinaikkan pada sebuah eksponen ganjil (x3 atau x5, dll.) dan memiliki koefisien utama positif ketika x mendekati +∞ fungsinya akan menjadi +∞, dan ketika x mendekati -∞ fungsinya akan secara terbalik menjadi -∞. Terakhir, jika sebuah fungsi dinaikkan pada sebuah eksponen ganjil (x3 atau x5, dll.) dan memiliki koefisien utama negatif ketika x mendekati -∞ fungsinya akan menjadi +∞, dan ketika x mendekati +∞ fungsinya akan secara terbalik menjadi -∞.
Sekarang, dengan pengetahuan ini, mari kita mencoba membuat grafik dari sebuah polinomial berikut ini: x3-6x2+3x+10
Pertama, dengan mengamati fungsinya, kita dapat melihat bahwa x=-1 adalah sebuah akar, jadi kita dapat menulis ulang polinomialnya menjadi (x+1)(x2-7x+10)
Selanjutnya, kita dapat memfaktorkan x2-7x+10 menjadi (x-5) (x-2), dan menulis ulang bentuk akhir menjadi (x+1) (x-5) (x-2).
Sekarang mari kita mulai membuat grafik fungsi kita, mencari akar-akar pada grafik kita di bawah ini:

Selanjutnya, dengan menggunakan pengetahuan kita tentang kelakuan (behavior), kita dapat menggambarkan sketsa kasar dari polinomial tersebut:

Dan begitulah. Jika kalian dapat mengetahui akar kalian, dan menggunakan pengetahuan kalian tentang kelakuan (behavior), akan menjadi sangat mudah untuk membuat grafik dari polinomial berapapun.
S1
Dapatkah kamu mengidentifikasi grafik polinomial fungsi f(x)?
f(x) = x 3 - 2x 2 - x + 2S2
Polinomial dengan 4 tingkatan mempunyai koefisiensi utama positif dan nol sederhana (nol dari kelipatan 1) di
x = 2, x = - 2, x = 1 dan x = -1. Maka perpotongan sumbu y pada grafiknya adalah:
S3
Grafik polinomial p ditunjukkan di bawah ini.

Apa yang bisa kamu katakan tentang derajat polinomial dan tanda dari koefisien utama?
S4
Grafik berikut adalah sebuah polinomial fungsi p(x) dengan koefisien riil. Derajat dari p(x) adalah 3 dan akarnya diasumsikan sebagai bilangan bulat. Maka p(x) adalah:

S5
Grafik manakah yang menggambarkan p(x)
dimana p(x) = x 4 - x 2 + 1?
dimana p(x) = x 4 - x 2 + 1?
S6
Grafik manakah yang menggambarkan p(x) =
x3 - 2x2 + 2x - 4?
x3 - 2x2 + 2x - 4?
S7
Grafik dari polinomial kubik y = a x 3 + b x 2 + c x + d ditunjukan di bawah ini. Temukan koefisien a, b, c dan d.

S8
Sebuah polinomial dengan koefisien riil dan derajat 5 mempunyai akar 0, 1, -1 dan 2(kelipataa 2).
p(3) = -12. Grafik yang menggambarkan p(x) adalah:
S9
Grafik polinomial y = a x 4 + b x 3 + c x 2 + d x + e ditunjukkan dibawah ini. Temukan nilai koefisien a, b, c, d dan e.

S10
Bisakah kamu mengidentifikasi grafik polinomial fungsi f(x)?

Tidak ada komentar:
Posting Komentar