Contoh Soal Pembagian polinomial - Di dalam pelajaran ini kita akan belajar mengenai bagaimana melakukan pembagian suku banyak polinomial.
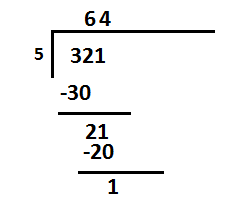
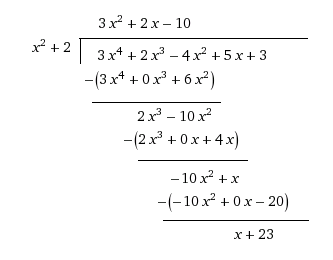
x 3 + x 2 ( x + 1 ) 2 + 3 x + 1
x 3 − y 3 , Q = x − y
x 5 + 4 x 3 − 2 x + 1 , Q = x 3 − 2
x 5 + 4 x 4 + 5 x 3 + 6 x 2 − 7 x + 8 , Q = x + 1
Tentang:
MIA kelas 11
Pertama mari kita mengingat bagaimana cara melakukan pembagian suku banyak reguler. Sebuah bilangan,n, disebut pembilang (dividend) dibagi oleh bilangan lain d yang disebut pembagi (divisor) yang menghasilkan hasil-bagi, q, dan sisa, r, dimana r<d dan n=d*q+r.
Mari kita lihat pada sebuah contoh,
Contoh 1: Bagi 321 dengan 5.
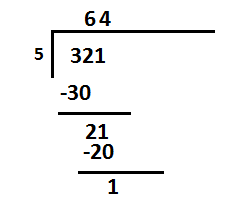
Maka 321=564+1. Dan kita melihat bahwa 64 adalah hasil-bagi dan 1 adalah sisa.
Sekarang kita dapat menerapkan ide yang sama pada polinomial. Catat bahwa tiap digit mewakili pangkat 10. Maka ketika kita melihat pada polinomial, kita akan memertimbangkan derajat dari polinomial tersebut. Derajat dari polinomial adalah pangkat tertinggi untuk sebuah suku. Juga ingat bahwa sebuah polinomial hanya dapat memiliki bilangan cacah sebagai pangkatnya.
Contoh 2: Berapa derajat dari polinomial berikut ini, x4-5x7+3x+15x3?
Karena derajat tertinggi adalah x7, derajat dari polinomial adalah 7.
Untuk melakukan pembagian polinomial: Sebuah polinomial, p(x), disebut pembilang (dividend) dibagi oleh polinomial lainnya d(x) disebut pembagi (divisor) yang menghasilkan hasil-bagi, q(x), dan sisa, r(x), dimana derajat dari r(x)< derajat d(x) dan p(x)=d(x)q(x)+r(x).
Akhirnya sekarang kita dapat melihat pada sebuah contoh pembagian suku-banyak polinomial yang kerjanya sangat mirip dengan pembagian suku-banyak reguler.
Contoh 3: Bagi 3x4+2x3-4x2+5x+3 by x2+2
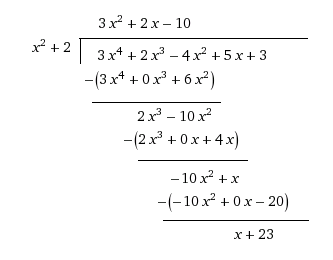
Maka kita melihat bahwa hasilnya adalah 3x2+2x-10 dengan sisa x+23. Dan kita menyatakan bahwa derajat dari sisa (1) adalah lebih rendah daripada derajat dari pembagi (2).
S1
Terdapat polinomial P yang diberikan di bawah. Berapakah derajat dari polinomial ini?
S2
Polinomial P berderajat 8 dibagi dengan polinomial berderajat 3, bagaimanakah urutan dari resultan hasil baginya? (Dengan asumsi bahwa hasil baginya adalah sebuah polinomial)
S3
Polinomial P berderajat 8 dibagi dengan polinomial Q berderajat 5. Berapakah derajat maksimal yang memungkinkan dari sisanya?
S4
Luas persegi panjang diumpamakan dengan polinomial x2 - x - 12. Jika panjang dari persegi panjangnya adalah x + 3, maka berapakah lebar dari persegi panjang tersebut?
S5
Luas sebuah segitiga siku-siku dinyatakan dengan polinomial x2 + 5x + 4. Panjang alas dari segitiga tersebut adalah x + 4 dan tinggi dari segitiganya adalah 6, berapakah nilai numerik dari luas segitiga tersebut?
S6
Dua persegi panjang dengan lebar yang sama ditempatkan bersebelahan. Luas dari persegi pertama adalah (x + 1)2 dan luas persegi kedua adalah x2 - 1. Jika panjang kombinasi kedua persegi panjang adalah 2x, manakah pilihan jawaban di bawah yang menggambarkan lebar persegi panjang?
S7
Polinomial P di bawah ini dibagi dengan polinomial Q. Berapakah hasil bagi dari kedua polinomial tersebut?
S8
Polinomial P dibagi dengan polinomial Q. Berapakah sisa dari pembagian tersebut?
S9
Volume sebuah balok adalah x3 + 12x2 + 42x + 49, luas dari alasnya adalah x2 + 5x + 7, Jika nilai numerik tingginya adalah 8, berapakah nilai numerik dari volumenya?
S10
Polinomial P dibagi oleh polinomial Q, berapakah sisa dari hasil pembagiannya?

ga ada kunci jawabannya kak?
BalasHapus