Contoh Soal Hubungan antara direktriks, titik fokus, dan titik-titik pada Parabola - Apakah kalian pernah mendengar istilah irisan kerucut? Salah satu irisan kerucut adalah bentuk parabola. Pada sebuah parabola terdapat garis dan titik yang saling berhubungan yang merupakan unsur-unsur penyusun parabola tersebut.
Untuk parabola yang puncaknya di titik (a,b) maka parabola semula berpuncak di titik (0,0) akan mengalami pergeseran sejauh :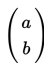
Selanjutnya, untuk persamaan parabola dengan bentuk y2 = 4px yang berpuncak di (0,0) digeser sejauh :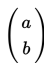
Mari kita cermati beberapa contoh berikut ini.
Contoh 1
Penyelesaian
Contoh 2
Penyelesaian
Tentang:
MIA kelas 11
Untuk mempelajari istilah-istilah dalam parabola, mari kita perhatikan beberapa contoh grafik fungsi parabola berikut ini.

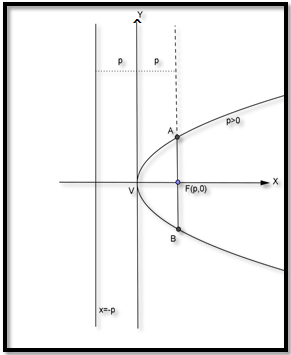
- Persamaan parabola : y2 = 4px
- Koordinat titik puncak : V(0,0)
- Koordinat titik fokus : F(p,0) -> Jika p > 0 maka parabola terbuka ke kanan
- Sumbu simetri : sumbu X
- Persamaan garis direktriks : x = -p
- Panjang latus rectum : AB = 4|p|

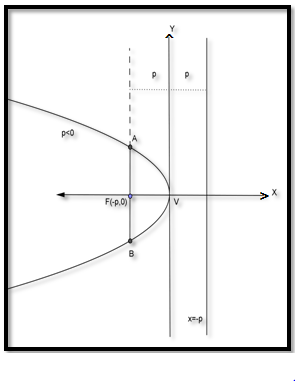
- Persamaan parabola : y2 = 4px
- Koordinat titik puncak : V(0,0)
- Koordinat titik fokus : F(-p,0) -> Jika p < 0 maka parabola terbuka ke kiri
- Sumbu simetri : sumbu X
- Persamaan garis direktriks : x = p
- Panjang latus rectum : AB = 4|p|

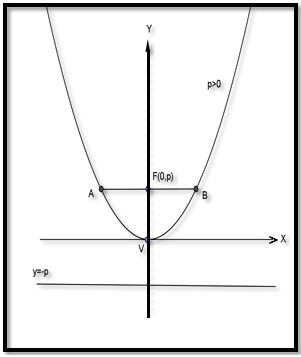
- Persamaan parabola : x2 = 4py
- Koordinat titik puncak : V(0,0)
- Koordinat titik fokus : F(0,p) -> Jika p > 0 maka parabola terbuka ke atas
- Sumbu simetri : sumbu Y
- Persamaan garis direktriks : y = -p
- Panjang latus rectum : AB = 4|p|

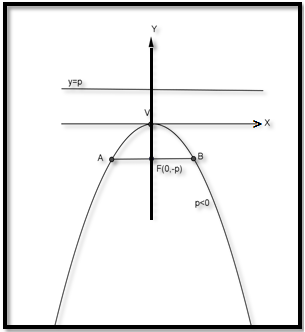
- Persamaan parabola : x2 = 4py
- Koordinat titik puncak : V(0,0)
- Koordinat titik fokus : F(0,-p) -> Jika p < 0 maka parabola terbuka ke atas
- Sumbu simetri : sumbu Y
- Persamaan garis direktriks : y = p
- Panjang latus rectum AB = 4|p|
Bagaimana cara memperoleh persamaan parabola yang puncaknya tidak terletak pada titik (0,0)?
Untuk parabola yang puncaknya di titik (a,b) maka parabola semula berpuncak di titik (0,0) akan mengalami pergeseran sejauh :
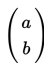
sehingga untuk persamaan parabola dengan bentuk x2 = 4py yang semula mempunyai puncak di titik (0,0) sekarang puncaknya terletak di titik (a,b) dan persamaan parabola menjadi (x - a)2 = 4p(y - b)
Selanjutnya, untuk persamaan parabola dengan bentuk y2 = 4px yang berpuncak di (0,0) digeser sejauh :
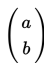
maka puncak koordinat puncak menjadi di titik (a,b) dan persamaan parabola menjadi :
(y - b)2 = 4p(x - a)
(y - b)2 = 4p(x - a)
Mari kita cermati beberapa contoh berikut ini.
Contoh 1
Tentukan persamaan garis direktriks dari parabola y2 = 8x
Penyelesaian
Persamaan parabola y2 = 8x sesuai dengan bentuk umum y2 = 4px dengan titik puncak di (0,0).
Karena 8x = 4px <=> p = 2 maka persamaan garis direktrisnya adalah x = -p <=> x = -2
Contoh 2
Tentukan persamaan parabola jika koordinat titik puncak (0,0), fokus (0,-1), dan sumbu Y adalah sumbu simetri!
Penyelesaian
Oleh karena puncak parabola (0,0) dan titik fokus adalah (0, -1) maka p = 1.
Dengan demikian, persamaan parabola yang dimaksud adalah x2 = 4y
Dengan demikian, persamaan parabola yang dimaksud adalah x2 = 4y
S1
Ronaldo menendang bola ke gawang lawan dengan persamaan (x+2)2 = -8(y-3) Koordinat titik fokus parabola adalah ….
S2
Persamaan parabola yang memiliki puncak di titik (2,4) dan titik fokus (5,4) adalah ….
S3
Persamaan parabola yang memiliki fokus (-4,-4) danpersamaan direktriks x= -5 adalah ….
S4
Persamaan parabola yang berpuncak di titik puncak O(0,0) dan melalui (6 , -6) serta menyinggung sumbu Y adalah…
S5
Persamaan parabola dengan puncak (0,0), sumbu simetri sumbu-x, fokus (-2,0) adalah …
S6
Lintasan bola basket yang berbentuk parabola dengan persamaan (y+4)2 = -4(x-2) Koordinat titik fokus parabola adalah ….
S7
Persamaan parabola yang memiliki puncak di titik (-3,4) dan titik fokus (-3,6) adalah ….
S8
Persamaan parabola yang memiliki fokus (5 , -2) dan persamaan direktriks x = 7 adalah ….
S9
Persamaan parabola dengan puncak O(0,0) , melalui titik (-3,6) , dan menyinggung sumbu Y adalah ….
S10
Persamaan parabola dengan puncak (0,0), sumbu simetrinya adalah sumbu Y, dan fokus (0 , -3) adalah ….

Tidak ada komentar:
Posting Komentar