Contoh Soal Menemukan persamaan lingkaran - Mencari Persamaan Lingkaran/b>
Carilah persamaan lingkaran yang terbentuk jika diketahui titik-titik ujung dari diameter lingkaran adalah (2, 4) dann(-2, 0)!
Tentang:
MIA kelas 11
Lingkaran didefinisikan sebagai the himpunan semua titik yang mempunyai jarak sama jika diukur dari titik pusat.
Jika titik pusat lingkaran adalah (a,b), maka semua titikyang mempunyai jarak sebesar r jika dihitung dari titik pusat (a,b) akan membentuk sebuah lingkaran.
Mari kita turunkan persamaan lingkaran dengan cara sebagai berikut :
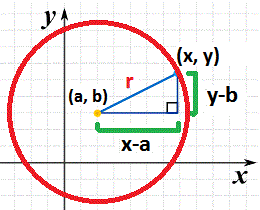
Buatlah sebuah segitiga siku-siku di dalam sebuah lingkaran, seperti yang ditunjukkan oleh gambar di bawah ini.

Dengan menggunakan theorema Phytagoras : (a2 + b2 = c2), diperoleh :
(x-a)2 + (y-b)2 = r2
yang mana merupakan"PERSMAAN LINGKARAN SECARA UMUM (BENTUK STANDAR)".
Catatan : seringkali persamaan lingkaran yang diberikan tidak dalam bentuk standar. Selanjutnya, dengan menjabarkan bentuk kuadrat dari persamaan lingkaran secara umum, maka diperoleh :
(x-a)2 + (y-b)2 = r2
x2 + a2 -2ax + y2 + b2 - 2by = r2
x2 + y2 - 2ax - 2by = r2 - a2 - b2
x2 + y2 - 2ax - 2by = r2 - a2 - b2
x2 + y2 - 2ax - 2by = c2
dimana c2 = r2 - a2 - b2
Dalam pelajaran ini, kalian akan belajar tentang bagaimana mencari persamaaan persamaan lingkaran jika diketahui jari-jari lingkaran atau titik pusat. Berikut ini adalah beberapa contoh yang akan membatu kalian dalam memahami materi ini :
CONTOH 1 :
Carilah persamaan lingkaran dengan titik pusat (4, -3) dan keliling sebesar 10π!
PENYELESAIAN :
Seperti yang telah kita ketahui, keliling lingkaran adalah
K = 2πr
Karena keliling lingkaran adalah 10π, maka r = 5 satuan panjang.
Dengan demikian. persamaan lingkaran yang dicari adalah :
(x-4)2 + (y+3)2 = 52
CONTOH 2 :
Carilah persamaan lingkaran yang terbentuk jika diketahui titik-titik ujung dari diameter lingkaran adalah (2, 4) dann(-2, 0)!
PENYELESAIAN :
Titik pusat lingkaran akan berada pada titik tengah dari diameter lingkaran.
Dengan demikian,
titik pusat lingkaran = ( (2-2)/2 , (4+0)/2 ) = (0, 2)
Selanjutnya, dengan menggunakan rumus jarak, panjang jari-jari lingkaran (r) dapat dicari dengan cara sebagai berikut :
r = √{ (2-0)2 + (4-2)2 } = 2√2
Jadi, persamaan lingkaran yg dicari adalah :
(x-0)2 + (y-2)2 = (2√2)2
ATAU x2 + y2 -4y = 8
S1
Persamaan lingkaran manakah dengan jari-jari r dan pusat (a,b)?
S2
Tentukan persamaan lingkaran dengan diameter 10 dan titik pusat (4, 3)!
S3
Berapakah persamaan lingkaran dengan titik pusat (-3, 2) dan luas 16π?
S4
Berapakah persamaan lingkaran dengan jari-jari cm dan titik pusat (3, 5)?
S5
Berapakah persamaan lingkaran yang melewati titik (2, 4) dan titik pusat sebagai titik potong
garis x – y = 4 dan 2x + 3y = -7?
S6
Berapakah persamaan lingkaran yang sepusat dengan lingkaran x2 + y2 - 4x - 6y - 3 = 0 dan menyinggung sumbux?
S7
Berapakah persamaan lingkaran dengan titik (3, 2) dan (-1, 6) sebagai titik ujung diameternya?
S8
Manakah yang merupakan persamaan lingkaran?
S9
Berapakah persamaan lingkaran yang melewati titik (2, –2), dan (3, 4) dengan titik pusat berada pada garis
x + y = 2?
S10
Berapakah persamaan lingkaran dengan titik pusat (2, -5) yang mempunyai jari-jari sama dengan lingkaran
x2 + y2 + 6x + 8y - 24 = 0?

Tidak ada komentar:
Posting Komentar