Contoh Soal Menyelesaikan dan menafsirkan solusi persamaan dalam sebuah konteks

Contoh Soal Menyelesaikan dan menafsirkan solusi persamaan dalam sebuah konteks - Di dalam pelajaran ini kita akan belajar mengenai bagaimana menyatakan soal-soal kalimat ke dalam persamaan  aljabar dan kemudian menyelesaikan persamaan tersebut. 

Menyatakan soal-soal kalimat ke dalam persamaan adalah salah satu hal yang paling sulit dilakukan dalam matematika. Umumnya, hal ini bukanlah proses berrumus dan membutuhkan pemikiran bukannya sebuah proses rute, yang membuatnya sulit. Di dalam pelajaran ini, kita akan membahas 3 tipe soal kalimat dan bagaimana menyatakannya ke dalam persamaan. Contoh soal ini mencakup setiap situasi yang akan memberi kalian awal yang cukup untuk memahami bagaimana melakukan pendekatan terhadap soal-soal jenis ini. Kita akan membahas soal garis-keliling, soal kecepatan (rate), dan soal perubahan persen.

Contoh 1: Soal garis-keliling.

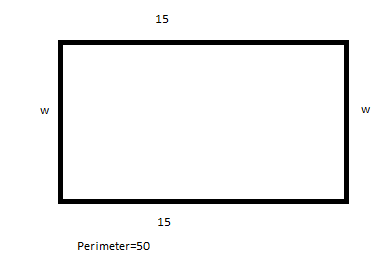
Misalnya garis-keliling dari sebuah persegi panjang adalah 50 meter dan salah satu sisinya adalah 15 meter. Berapa panjang sisi yang lain?

Karena ini adalah soal garis-keliling, kita akan mulai dengan garis-keliling dari rumus persegi panjang. Yaitu, 2panjang+2lebar=keliling. Jika kalian tidak dapat mengingat rumus keliling cobalah membuat gambar seperti yang ditunjukkan di bawah ini dan ingat bahwa keliling adalah jumlah sisi-sisinya. 

Sekarang, kita diberi dua variabel yaitu panjang dan keliling. Karena persamaan kita adalah,

2*15+2*w=50 dimana w=lebar

Sekarang carilah w,

30+2w=50

2w=20

w=10

Maka sisi satunya mempunyai ukuran 10 meter. 

Contoh 2: Soal Kecepatan

Charlie membutuhkan waktu 5 jam untuk menyelesaikan sebuah pekerjaan. Tapi Amy hanya butuh waktu 2 jam untuk menyelesaikan pekerjaan yang sama. Berapa lama waktu yang dibutuhkan oleh kedua saudara ini bila bekerja bersama-sama?

Untuk soal kecepatan kita harus selalu ingat bahwa jarak=kecepatan*waktu. Maka jaraknya adalah penyelesaian dari 1 pekerjaan, maka jaraknya adalah 1. Strategi kita adalah terlebih dulu menemukan kecepatan masing-masing orang dari dua bersaudara itu dan kemudian mencari waktu yang dibutuhkan mereka untuk bekerja bersama-sama

Kecepatan Charlie: dc=rc*tc, jadi 1=rc*5 dan rc=1/5

Kecepatan Amy: da=ra*ta, jadi 1=ra*2 dan ra=1/2

Sekarang kecepatan mereka berdua dalam bekerjasama adalah 1/5+1/2=2/10+5/10=7/10

Maka kita mendapatkan: 1=(7/10)*t

Penyelesaian untuk t=10/7 jam. 

Contoh 3: Soal perubahan persen.

Pada tahun 1999 Smalltowne memiliki populasi 1000 orang. Pada tahun 2000, populasi Smalletowne sebesar 1500 orang. Berapa persen pertumbuhan yang terjadi di Smalltowne antara tahun 1999 dan 2000?

Ini adalah soal perubahan persen jadi kita perlu menggunakan rumus perubahan persen,

Perubahan persen=(akhir-awal)/awal

Untuk soal ini, akhirnya adalah 1500 dan awalnya adalah 1000. Maka,

Perubahan persen=(1500-1000)/1000=500/1000=.5=50%.

Sehinggga populasi di Smalltowne tumbuh sebesar 50% mulai dari 1999 hingga 2000.

Soal-soal diatas hanyalah 3 contoh soal mengenai cara menyatakan soal-soal kalimat ke dalam persamaan. Tapi perhatikan bahwa untuk semua contoh di atas kita terlebih dulu harus mengembangkan sebuah hubungan antara bagian-bagian informasi yang ada dan kemudian bekerja dari sana untuk menemukan apa yang hilang. Membutuhkan banyak latihan untuk mengasah keahlian ini. 

S1

Keliling sebuah persegi panjang adalah 44cm dan kedua sisinya mempunyai panjang 10cm. Berapa panjang dari dua sisi lain dari persegi panjang tersebut?

S2

Seorang gadis, A, memerlukan waktu 5 jam untuk mengecat dinding. Temannya, B, butuh waktu dua kali lipat dari A untuk mengecat dinding dengan dimensi yang sama. Berapa lama akan tugas yang dilakukan gadis-gadis itu jika mereka bekerja bersama?

S3

Pada tahun 2004, anggaran katering bulanan sebuah hotel adalah $2000. Pada tahun 2009 anggaran bulanan ditingkatkan sampai $4200. Berapakah persentase kenaikan anggaran bulanan dari tahun 2004 sampai 2009?

S4

Seorang guru mengendarai sepeda. Salah satu bannya bocor di dua titik. Satu kebocoran saja bisa membuat ban kempes dalam waktu menit 8. Kebocoran yang lain bisa membuat ban kempes dalam waktu 5 menit. Berapa lama waktu yang dibutuhkan kedua kebocoran bersamaan untuk membuat ban kempes (sampai 0.5 menit terdekat)?

S5

Dalam pembuatan pemukul baseball, biaya kayu adalah $x dan biaya proses manufakturnya seperempat dari biaya kayu. Berapakah biaya $ pembuatan 100 pemukulan baseball dalam $?

S6

Seorang penjaga toko menjual 100 buku pertamanya dengan harga masing-masing $80 dan kemudian menjual sisa buku dengan harga masing-masing $x. Jika ia menjual 250 buku untuk total pendapatan $14500, berapakah harga x (sampai ke $ terdekat)?

S7

Sejumlah x orang disurvei dan ditemukan bahwa 65% orang menyukai produk A. Setelah itu, tambahan orang sejumlah y disurvei dan mereka semua menyukai produk A. Pada akhir survei itu diketahui bahwa 75% dari semua partisipan menyukai produk A. Carilah y dalam bentuk suku bilangan x

S8

Seorang pemilik bisnis telah menginvestasikan uang ke dalam dua perusahaan yang berbeda. Pada perusahaan pertama ia menginvestasikan uang dengan bunga tahunan 5% dan di perusahaan kedua ia investasikan dengan bunga 8%. Jika dia menginvestasikan $ 1000 lebih sedikit ke perusahaan pertama dibandingkan perusahaan kedua dan pendapatan tahunannya dari kedua investasi itu adalah $ 100, berapa banyak dia berinvestasi di perusahaan kedua?

S9

Jika jumlah tiga bilangan bulat genap berurutan adalah 210 maka berapakah jumlah
dua bilangan bulat yang lebih kecil?

S10

Seorang guru menginvestasikan $2000 ke sebuah bank dengan bunga tahunan 5%. Berapa banyak lagi yang perlu ia
investasikan pada suku bunga tahunan 3% jika ia ingin total investasinya untuk menghasilkan 4%?

Tentang: MIA kelas 11

Share:

Artikel Terkait