Aturan Sinus dan Cosinus Dalam Konteks - Pada pelajaran sebelumnya kamu telah belajar bagaimana cara menggunakan aturan sinus dan cosinus untuk menyelesaikan masalah sederhana tentang segitiga.
Sekarang, kamu akan mengetahui bagaimana cara menggunakan aturan sinus dan cosinus ini untuk menyelesaikan masalah sehari-hari yang rumit.
Penjelasan
Untuk menentukan ketinggian satelit, kita harus menentukan jarak dari satelit ke satu pamancar terlebih dahulu, dalam meter.
Contoh 2
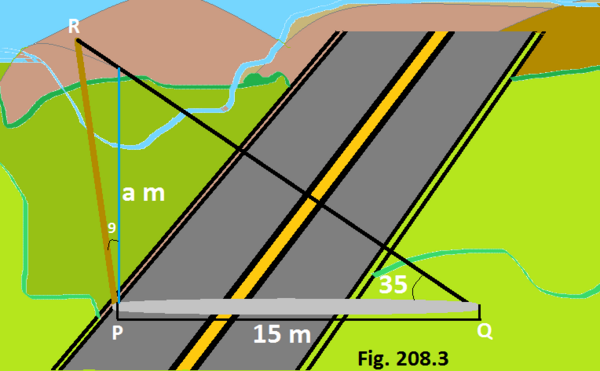
Suatu tiang memiliki kemiringan ke arah matahari dengan sudut 9∘, sehingga terbentuk bayangan tiang sepanjang 15 m di atas tanah. Sudut elevasi dari ujung bayangan ke puncak tiang adalah 35∘. Berapa panjang tiang tersebut?
A 12 m
B 10 m
C 15 m
D 19m
E 20 m
Answer A
Penjelasan
Kita awali dengan menggambar sketsa yang sesuai dengan situasi yang diberikan soal. [Lihat Gb. 208.3].
Dari Gb. 208.3 kamu dapat mengetahui bahwa kita perlu menentukan tiang yan normal agar dapat menentukan panjangnya. Sehingga, kita menggunakan teorema Pythagoras untuk menentukan 'a' sebagai berikut:
tan(35∘) = a/15
a ≈ 10.5 m
Tentang:
Matematika
 |
| Aturan Sinus dan Cosinus Dalam Konteks |
Ingat bahwa aturan sinus dan cosinus ini dapat dirubah bentuknya untuk menentukan suatu sudut atau panjang sisi berdasarkan masalah yang diberikan pada soal.[Gb. 208.1] Ada banyak cara yang dapat dilakukan untuk menyelesaikan masalah dengan menggunakan aturan yang sama .
Sekarang, kamu akan mengetahui bagaimana cara menggunakan aturan sinus dan cosinus ini untuk menyelesaikan masalah sehari-hari yang rumit.

Ingat bahwa saat kamu menyelesaikan soal segitiga, kamu perlu untuk membuat sketsa diagram dengan hati-hati untuk memeriksa adanya kemungkinan dari solusi peta berpikirmu dan jawabanmu.
Contoh 1
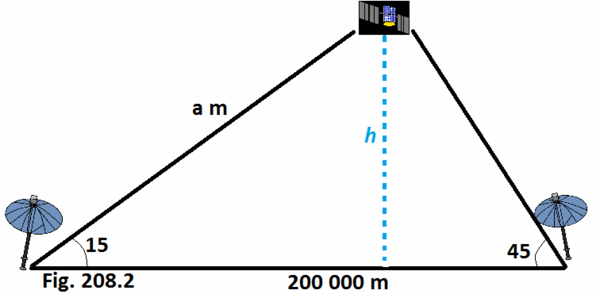
Dua pemancar radar terletak pada ktinggian 200 000 meter di atas permukaan laut mendeteksi sinyal satelit dari langit. Sudut elevasi dari pemancar pertama adalah 15∘. Sudut elevasi dari pemancar kedua adalah 45∘. Berapa ketinggian satelit dari permukaan tanah?
A 163 000 m
B 43 000 m
C 162 000 m
D 42 000 m
E 41 000 m
Contoh 1
Dua pemancar radar terletak pada ktinggian 200 000 meter di atas permukaan laut mendeteksi sinyal satelit dari langit. Sudut elevasi dari pemancar pertama adalah 15∘. Sudut elevasi dari pemancar kedua adalah 45∘. Berapa ketinggian satelit dari permukaan tanah?
A 163 000 m
B 43 000 m
C 162 000 m
D 42 000 m
E 41 000 m
Jawaban D
Penjelasan
Untuk menentukan ketinggian satelit, kita harus menentukan jarak dari satelit ke satu pamancar terlebih dahulu, dalam meter.
Kemudian menggunakan Teorema Pythagoras untuk menemukan 'h'.
Ingat bahwa jumlah semua sudut dalam segitiga adalah 180∘. Oleh karena itu, sudut yang tidak diketahui dari segitiga adalah
180∘ - 45∘ - 15∘ = 120∘
Sudut ini adalah sudut di hadapan alas segitiga yang memiliki jarak di antara keduanya. Sehingga kita perlu menggunakan aturan sinus untuk menentukan jarak antara satelit dengan satu pemancar :
Ingat bahwa jumlah semua sudut dalam segitiga adalah 180∘. Oleh karena itu, sudut yang tidak diketahui dari segitiga adalah
180∘ - 45∘ - 15∘ = 120∘
Sudut ini adalah sudut di hadapan alas segitiga yang memiliki jarak di antara keduanya. Sehingga kita perlu menggunakan aturan sinus untuk menentukan jarak antara satelit dengan satu pemancar :

a/sinA = b/sinB
200 000/sin(120∘ ) = a/sin(45∘ )
a = 163299.3 ≈ 163000 m.
Sehingga, jarak antara satelit dan satu pemancar adalah163000 m.
Sekarang kita dapat mengetahui 'a', kita perlu menggunakan teorema Pythagoras untuk menentukan ketinggian 'h' dari satelit.
sin(15∘) = h/a
sin(15∘) = h/163000
h = 42187.5 ≈ 42000 m
200 000/sin(120∘ ) = a/sin(45∘ )
a = 163299.3 ≈ 163000 m.
Sehingga, jarak antara satelit dan satu pemancar adalah163000 m.
Sekarang kita dapat mengetahui 'a', kita perlu menggunakan teorema Pythagoras untuk menentukan ketinggian 'h' dari satelit.
sin(15∘) = h/a
sin(15∘) = h/163000
h = 42187.5 ≈ 42000 m
Contoh 2
Suatu tiang memiliki kemiringan ke arah matahari dengan sudut 9∘, sehingga terbentuk bayangan tiang sepanjang 15 m di atas tanah. Sudut elevasi dari ujung bayangan ke puncak tiang adalah 35∘. Berapa panjang tiang tersebut?
A 12 m
B 10 m
C 15 m
D 19m
E 20 m
Answer A
Penjelasan
Kita awali dengan menggambar sketsa yang sesuai dengan situasi yang diberikan soal. [Lihat Gb. 208.3].
Dari Gb. 208.3 kamu dapat mengetahui bahwa kita perlu menentukan tiang yan normal agar dapat menentukan panjangnya. Sehingga, kita menggunakan teorema Pythagoras untuk menentukan 'a' sebagai berikut:
tan(35∘) = a/15
a ≈ 10.5 m
Sekarang, ∢P = 90∘ + 9∘ = 99∘
∢R = 180∘ - 35∘ - 99∘ = 46∘
Dengan menggunakan aturan sinus, kita dapatkan
r/sinR = b/sinB
15/(sin46∘) = PR/(sin 35∘)
PR = 11.96 ≃ 12 mDengan menggunakan aturan sinus, kita dapatkan
r/sinR = b/sinB
15/(sin46∘) = PR/(sin 35∘)

Kita dapat menggunaka aturan cosinus untuk menyelesaikan masalah sehari-hari.
Contoh 3
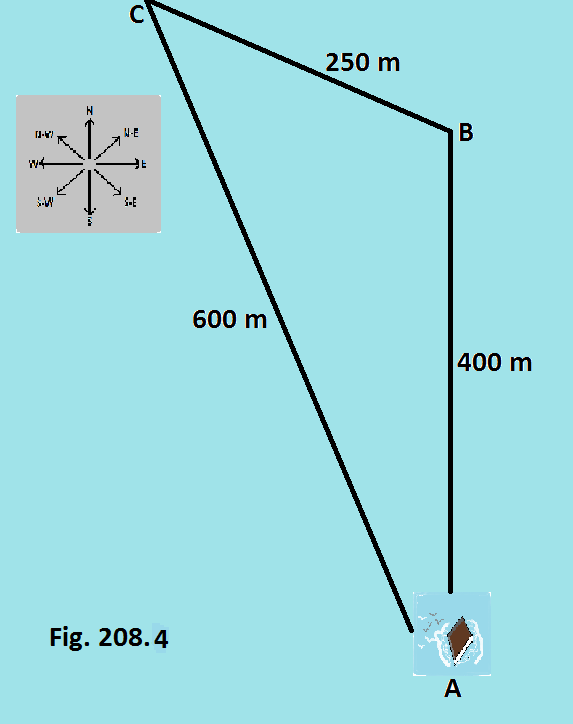
Sebuah kapal berjalan 400 meter ke arah Utara, berbelok ke arah Barat Laut dan berjalan sejauh 250 meter. Kemudian berbelok ke arah Tenggara dan berjalan sejauh 600 meter kembali ke posisi semula.Tentukan sudut pada belokan pertama ke arah Barat Laut.
A 17.6∘ N-W
B 133.4∘ N-W
C 133.4∘ W
D 17.6∘ W
E 17.6∘ S
Jawaban B
Penjelasan
Kita mulai dengan membuat diagram sederhana [Lihat Gb. 208.4] seperti pada contoh sebelumnya.
Contoh 3
Sebuah kapal berjalan 400 meter ke arah Utara, berbelok ke arah Barat Laut dan berjalan sejauh 250 meter. Kemudian berbelok ke arah Tenggara dan berjalan sejauh 600 meter kembali ke posisi semula.Tentukan sudut pada belokan pertama ke arah Barat Laut.
A 17.6∘ N-W
B 133.4∘ N-W
C 133.4∘ W
D 17.6∘ W
E 17.6∘ S
Jawaban B
Penjelasan
Kita mulai dengan membuat diagram sederhana [Lihat Gb. 208.4] seperti pada contoh sebelumnya.

Gunakan aturan cosinus
cosB = ( a2 + c2 - b2 ) / 2ac
= ( 2502 + 4002 - 6002 ) / 2(250)(400)
cosB = -0.6875
∢B = 133.4∘
Oleh karena itu, sudut pada belokan pertama kapal adalah 133.4∘,ke arah Barat Laut.
cosB = ( a2 + c2 - b2 ) / 2ac
= ( 2502 + 4002 - 6002 ) / 2(250)(400)
cosB = -0.6875
∢B = 133.4∘
Oleh karena itu, sudut pada belokan pertama kapal adalah 133.4∘,ke arah Barat Laut.
Tidak ada komentar:
Posting Komentar