Diagram Kotak dan Diagram Batang-dan-Daun - Diagram batang - daun akan mirip dengan diagram titik yang kita pelajari pada pelajaran sebelumnya (pelajaran 243). Namun, diagram batang - daun penggunaan angka numerik untuk menampilkan data ketimbang menggunakan garis dan titik.
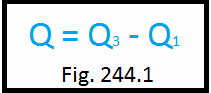
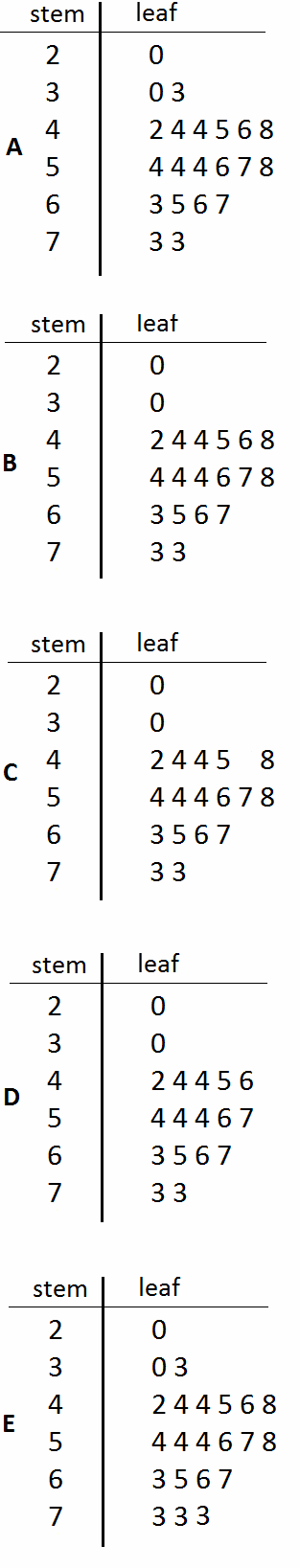

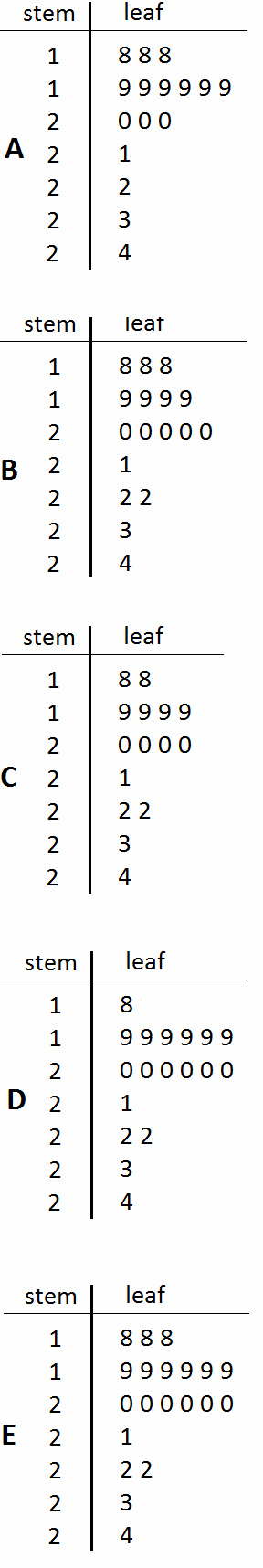
Tentang:
Matematika
 |
| Diagram Kotak dan Diagram Batang-dan-Daun |
Untuk menyusun sebuah diagram batang – daun, masing-masing bagian, yaitu sebuah batang dan sebuah daun dihasilkan dari masing-masing nilai. Sebagai contoh, angka 43 digambarkan seperti berikut “
batang daun
4 3
MedianMedian dihitung dengan menggunakan dua cara::
1. Jika banyaknya angka-angka adalah genap, maka median diperoleh dengan cara mengambil nilai rata-rata dari dua angka yang berada di tengah-tengah distribusi.
batang daun
4 3
MedianMedian dihitung dengan menggunakan dua cara::
1. Jika banyaknya angka-angka adalah genap, maka median diperoleh dengan cara mengambil nilai rata-rata dari dua angka yang berada di tengah-tengah distribusi.
2. Jika banyaknya angka-angka tersebut adalah ganjil, maka mediannya adalah angka yang berada di tengah-tengah.
Sebagaimana di kurva grafis, dimana data diplot berdasarkan frekuensi, kita tidak serta merta menemukan rata-rata, nilai tengah dan nilai terbanyak sebagaimana yang kita lakukan pada diagram batang-daun. Median akan membagi data menjadi dua bagian yang sama besar. Untuk membaginya menjadi dua bagian, kita harus melebarkannya dengan tiga garis sedemikian hingga kita memperoleh empat bagian yang sama besar.
Sebagaimana di kurva grafis, dimana data diplot berdasarkan frekuensi, kita tidak serta merta menemukan rata-rata, nilai tengah dan nilai terbanyak sebagaimana yang kita lakukan pada diagram batang-daun. Median akan membagi data menjadi dua bagian yang sama besar. Untuk membaginya menjadi dua bagian, kita harus melebarkannya dengan tiga garis sedemikian hingga kita memperoleh empat bagian yang sama besar.
Nilai tengah dari tengahan bawah disebut kuartil bawah, Q1, dan nilai tengahan dari tengahan atas disebut kuartil atas. and the middle value of the upper-half is called the upper-quartile, Q3. Kita harus ingat bahwa setiap bagian mewakili 25 % dari himpunan data.
Terlebih lagi, untuk memberi indikasi untuk sebaran angka relatif dalam himpunan angka, kita perlu untuk menghitung jangkauan interkuartil. [Fig. 244.1]
Jangkauan interkuartil = Kuartil atas – kuartil bawah
Di lain pihak, Jangkauan = Nilai tertinggi – nilai terendah
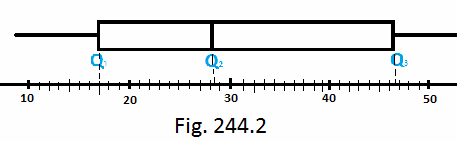
Diagram kotak digunakan untuk menjelaskan kuartil dan median dari suatu himpunan data pada sebuah garis bilangan atau grafik. [contoh Fig 244.2]
Diagram kotak digunakan untuk menjelaskan kuartil dan median dari suatu himpunan data pada sebuah garis bilangan atau grafik. [contoh Fig 244.2]
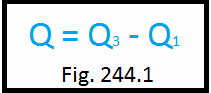

Pada Fig. 244.2, kuartil bawah adalah 17 dan kuartil atas adalah 46.5, jadi, jangkauan interkuartil = 46.5 - 17 = 29.5, dimana Q2 adalah median. Oleh karena itu, mediannya ada;aj 28.5
Contoh 1
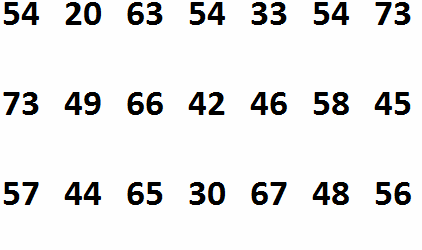
Data berikut menyajikan rentang waktu perhatian pada anak-anak sekolah menengah (dalam satuan menit).
Contoh 1
Data berikut menyajikan rentang waktu perhatian pada anak-anak sekolah menengah (dalam satuan menit).

Lihatlah yang manakah diagram batang-daun.
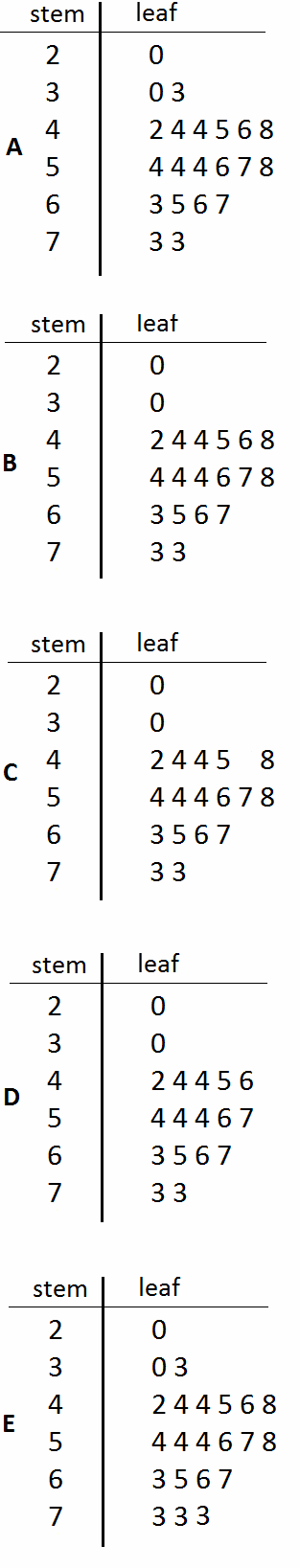
Jawaban: A.
Penjelasan :Pertama, kita mengatur ulang angka-angka secara menurun ataupun meningkat. . Tempatkan nilai-nilai tersebut pada diagram batang-daun secara bersesuaian dengan nilai-nilai yang ada pada himpunan data..
Contoh 2
Berikut kami berikan jumlah coklat yang ada pada masing-masing 20 keranjang.
Penjelasan :Pertama, kita mengatur ulang angka-angka secara menurun ataupun meningkat. . Tempatkan nilai-nilai tersebut pada diagram batang-daun secara bersesuaian dengan nilai-nilai yang ada pada himpunan data..
Contoh 2
Berikut kami berikan jumlah coklat yang ada pada masing-masing 20 keranjang.

Nyatakan manakah representasi yang tepat pada diagram batang-daun.
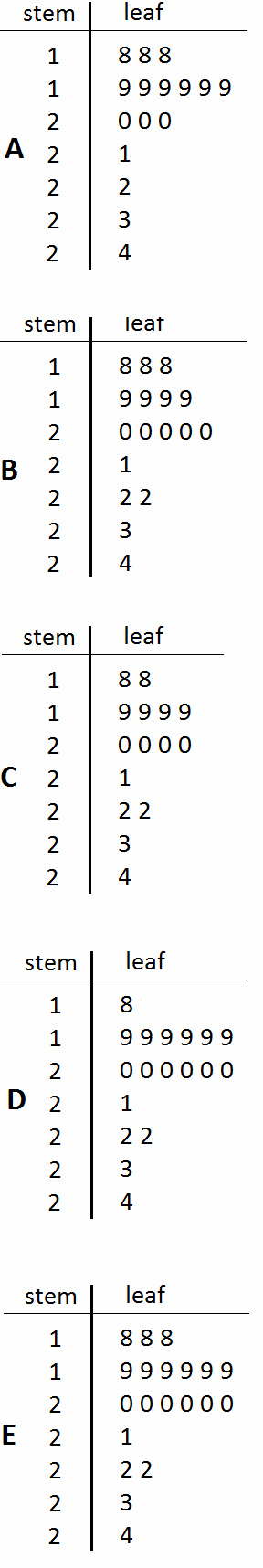
Jawaban E
Penjelasan
Pertama, kita atur ulang data-datanya secara menurun atau meningkat. Tempatkan nilai-nilai tersebut pada diagram batang-daun secara bersesuaian dengan nilai-nilai yang ada pada himpunan data.
Contoh 3
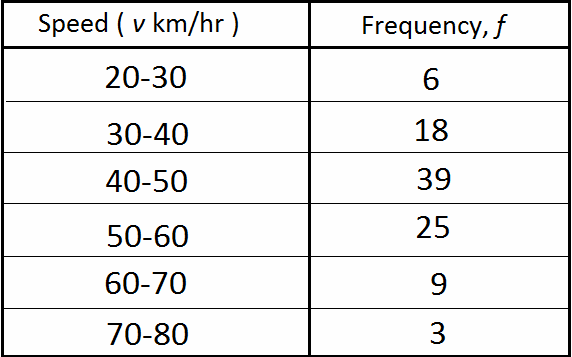
Tabel berikut menunjukkan kecepatan dari 100 kendaraan bermotor pada suatu titik di jalanan ramai.
Penjelasan
Pertama, kita atur ulang data-datanya secara menurun atau meningkat. Tempatkan nilai-nilai tersebut pada diagram batang-daun secara bersesuaian dengan nilai-nilai yang ada pada himpunan data.
Contoh 3
Tabel berikut menunjukkan kecepatan dari 100 kendaraan bermotor pada suatu titik di jalanan ramai.

Nyatakan manakah representasi yang tepat pada diagram batang-daun.
Nyatakan juga median, kuartil bawah dan kuartil atas dari kecepatan
Nyatakan juga median, kuartil bawah dan kuartil atas dari kecepatan

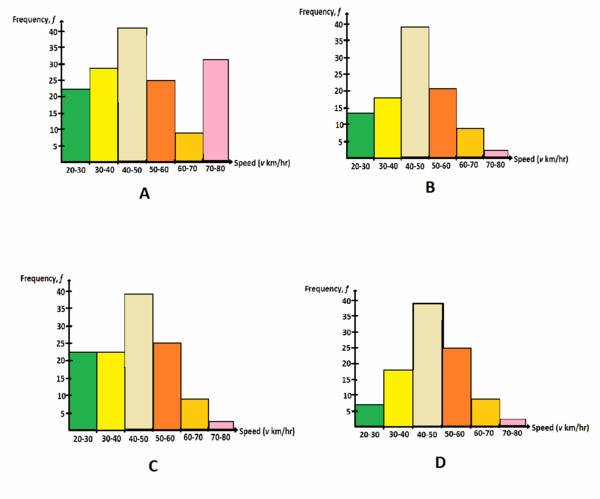
Jawaban E
Penjelasan
Pertama, kita atur ulang data-datanya secara menurun atau meningkat. Tempatkan nilai-nilai tersebut pada diagram batang-daun secara bersesuaian dengan nilai-nilai yang ada pada himpunan data. Plot the stem and leaf corresponding to the data values in the data set.
Contoh 3
Tabel berikut menunjukkan kecepatan dari 100 kendaraan bermotor pada suatu titik di jalanan ramai.
Jawaban D
Penjelasan
tinggi dari batangan berkorespondensi dengan kecepatan adalah proporsional dengan frekuensi data yang diberikan pada table. nbsp;
Untuk median dan kuartil, tuliskan semua rentang kecepatan pada urutan meningkat:
20-30, 20-30, 20-30, 20-30, 20-30, 20-30, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 40-50Q1, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50,40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50,median 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60Q3, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 60-70, 60-70, 60-70, 60-70, 60-70, 60-70, 60-70, 60-70, 60-70, 70-80, 70-80, 70-80.
Oleh karena itu, kuartil bawahnya adalah (40-50) km/h dan kuartil atas adalah (50-60) km/h,
dilain pihak, nilai tengah dari kecepatannya adalah (40-50) km/h untuk setiap 100 kendaraan.
Penjelasan
Pertama, kita atur ulang data-datanya secara menurun atau meningkat. Tempatkan nilai-nilai tersebut pada diagram batang-daun secara bersesuaian dengan nilai-nilai yang ada pada himpunan data. Plot the stem and leaf corresponding to the data values in the data set.
Contoh 3
Tabel berikut menunjukkan kecepatan dari 100 kendaraan bermotor pada suatu titik di jalanan ramai.
Jawaban D
Penjelasan
tinggi dari batangan berkorespondensi dengan kecepatan adalah proporsional dengan frekuensi data yang diberikan pada table. nbsp;
Untuk median dan kuartil, tuliskan semua rentang kecepatan pada urutan meningkat:
20-30, 20-30, 20-30, 20-30, 20-30, 20-30, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 30-40, 40-50Q1, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50,40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50,median 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 40-50, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60Q3, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 50-60, 60-70, 60-70, 60-70, 60-70, 60-70, 60-70, 60-70, 60-70, 60-70, 70-80, 70-80, 70-80.
Oleh karena itu, kuartil bawahnya adalah (40-50) km/h dan kuartil atas adalah (50-60) km/h,
dilain pihak, nilai tengah dari kecepatannya adalah (40-50) km/h untuk setiap 100 kendaraan.
Tidak ada komentar:
Posting Komentar