Garis Singgung Lingkaran

Garis Singgung Lingkaran - Pada materi sebelumnya sudah dipelajari bahwa suatu garis y = mx + n akan menyinggung lingkaran L = x2 + y2 = r2 jika diskriminan dari perpotongan garis dan lingkarannya sama dengan nol. Persamaan garis singgung lingkaran dapat ditentukan melalui titik pada lingkaran, melalui titik di luar lingkaran, atau jika gradien garis singgungnya diketahui.

Garis Singgung Lingkaran

Persamaan Lingkaran Melalui Titik Pada Lingkaran

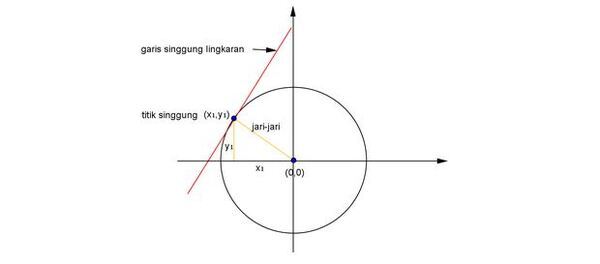
Misalkan diketahui titik (x1,y1) terletak pada lingkaran x2 + y2 = r2. Perhatikan bahwa (x1,y1) merupakan titik singgung dari singgung lingkaran tersebut.

Pada lingkaran x2 + y2 = r2 , lingkaran melalui (x1, y1) sehingga berlaku x12 + y12 = r12.

Contoh:

Tentukan persamaan garis singgung lingkaran x2 + y2 = 41 di titik (-4,5) !

Pembahasan:

Titik (-4,5) berada pada lingkaran x2 + y2 = 41 sehingga persamaan garis singgungnya:

x1x + y1y = r2

-4x + 5 y = 41

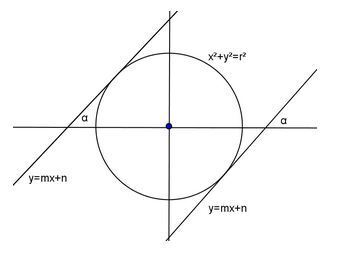
Persamaan Garis Singgung Lingkaran dengan Gradien m

Perhatikan gambar berikut:

Misalkan diketahui garis y = mx + n dengan gradien m dan lingkaran x2 + y2= r2.

Substitusi persamaan garis ke dalam persamaan lingkaran didapat:

x2 + (mx + n)2 = r2

x2 + m2x2 + 2mnx + n2 = r2

(1 + m2)x2 + 2mnx + n2 = r2

Garis y = mx + n menyinggung lingkaran x2 + y2= r2 jika D = 0.

(2mn)2 - 4(1 + m2 )(n2 - r2 ) = 0

4m2n2 - 4n2 + 4r2 - 4m2n2 + 4m2r2 = 0

4(n2 - r2 - m2r2 ) = 0

n2 = r2 + m2r2

n2 = r2 (1 + m2 )

n = ± r 1+m2‾‾‾‾‾‾‾√$\sqrt{1+m^2}$

Subsitusikan n = ± r 1+m2‾‾‾‾‾‾‾√$\sqrt{1+m^2}$ ke persamaan garis y = mx + n sehingga didapat:

y = mx ± r 1+m2‾‾‾‾‾‾‾√$\sqrt{1+m^2}$

Jadi, persamaan garis singgung lingkaran x2 + y2 = r2 dengan gradien m adalah:

y = mx ± r 1+m2‾‾‾‾‾‾‾√$\sqrt{1+m^2}$

Pada lingkaran yang berpusat di (a, b) yaitu (x - a)2 + (y - b)2 = r2 dengan gradien m, persamaan garis singgungnya adalah:

y - b = m(x - a) ± r 1+m2‾‾‾‾‾‾‾√$\sqrt{1+m^2}$

Contoh:

Tentukan persamaan garis singgung lingkaran x2 + y2 = 36 yang tegak lurus garis
x - 2y - 5 = 0 !

Persamaan Garis Singgung Lingkaran yang Melalui Sebuah Titik (x,y) di Luar Lingkaran

Contoh:

Tentukan persamaan garis singgung lingkaran melalui (1,5) pada lingkaran x2 + y2 = 25 !

Pembahasan:

Titik (1,5) jika disubstitusikan ke persamaan nilainya > 20, artinya titik tersebut berada di luar lingkaran. Persamaan garis singgung yang melalui (1,5) adalah

y -5 = m(x - 1)
y = mx - m + 5

Substitusikan y = mx - m + 5 ke persamaan x2 + y2 = 25 sehingga didapat

x2 + (mx - m + 5)2 = 25
x2 + m2x2 - 2m2x + m2 + 10mx - 10m + 25 = 25
(1 + m2)x2 + (-2m2 + 10m)x + m2 - 10m = 0

Karena garis menyinggung lingkaran maka D = 0 .

Tentang: Matematika

Share:

Artikel Terkait