Perpotongan Fungsi-fungsi Linier - Jika grafik-grafik dari dua fungsiberpotongan, ini berarti mereka melewati satu (atau lebih) titik yang sama . Ada dua metode untuk mencari koordinat titik potong.


Tentang:
Matematika
 |
| Perpotongan Fungsi-fungsi Linier |
Metode pertama adalah dengan menggambar grafik kedua fungsi , dan melihat di mana mereka saling silang (atau menggunakan kalkulator grafik untuk menemukan satu (atau lebih) titik potong).
Metode kedua adalah mengatur kedua fungsi tersebut menjadi sama satu dengan yang lain, lalu selesaikan persamaan baru ini untuk x, dan kemudian mensubstitusikan nilai ini kembali ke salah satu fungsi untuk menemukany.Mari kita lihat kedua metode di atas dalam contoh berikut.
Contoh 1
Diketahui f(x) = 2x + 1 dan g(x) = x + 6. Cari lah perpotongan pada grafik-grafik dari kedua fungsi.
Metode 1
Untuk mencari perpotongan dengan grafik, gambarlah grafik kedua fungsi tersebut dan sebutkan koordinat titik di mana kedua grafik berpotongan. Dalam grafik di bawah ini, tampak bahwa mereka berpotongan pada titik (2, 5).

Untuk meyakinkan jawaban ini, kita masukkan nilai 2 untuk x di dalam kedua fungsi untuk melihat apakah nilai fungsi (nilai y) adalah 5.
f(2) = 2(2) + 1
f(2) = 5
g(2) = (2) + 6
g(2) = 5
Titik tersebut terdapat di kedua fungsi, sehingga titik itu adalah benar merupakan titik potong.
Metode 2
Untuk menemukan perpotongan dua buah fungsi secara aljabar, kita ingin menemukannya ketika f (x) = g (x). Atur kedua fungsi tersebut menjadikannya sama satu dengan yang lain dan carilah nilai x,
2x + 1 = x + 6
4x + 2 = -x + 12
5x = 10
x = 2
Sekarang, masukkan nilai x ke dalam salah satu dari persamaan untuk menemukan koordinat y dari titik potong.Ini adalah ide bagus untuk memasukkan kekeduapersamaan untuk memeriksa pekerjaan kita.) Seperti yang kita lihat dalam metode 1, masukkan 2 ke dalam kedua fungsi maka didapatkan 5 sebagai hasil dari keduanya.
Jika terdapat dua fungsi yang merupakan garis sejajar satu sama lain, mereka tidak akan memiliki titik potong. Ada situasi lain di mana tidak ada titik potong, seperti yang akan kita lihat dalam contoh berikut.
Contoh 2
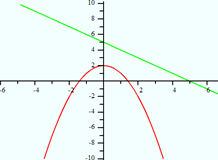
Temukan titik potong untuk fungsi f(x) = -x2 + 2 dan g(x) = -x + 5.
Jika kita coba mengatur kedua fungsi yang sama untuk mendapatkan x, akan menjadi:
-x2 + 2 = -x + 5
x2 – x + 3 = 0
Dengan menggunakan rumus kuadrat untuk menyelesaikan x,kita temukan bahwa xmerupakan bilangan imajiner. Oleh karena itu, kedua fungsi tidak berpotongan.
Hal ini dapat dipastikan dengan menggunakan grafik:

Permasalahan di dunia nyata sering dapat diselesaikan dengan mencari perpotongan dua fungsi, seperti yang terlihat dalam contoh berikut.
Contoh 3
Hasil produksi di sebuah pabrik dapat dimodelkan dengan persamaan f(x) = -x2 + 30x, dimana x adalah jumlah pekerja pada satu waktu, dan f(x)adalah jumlah unit yang diproduksi. Jika pabrik harus menghasilkan sedikitnya 200 unit, berapa jumlah minimum dan maksimum dari pekerja yang dibutuhkan untuk memenuhi tujuan produksi mereka?
Fungsi pertama diberikan kepada anda: f(x) = -x2 + 30x. Fungsi kedua adalah agak tersembunyi. Jika jumlah unit yang diproduksi harus di atas 200, maka g(x) = 200 adalah fungsi kedua. Lihatlah grafik untuk kedua fungsi.

Garis merah menunjukkan produksi, dan garis hijau menunjukkan produksi 200 unit. Kita perlu menemukan titik potong dari kedua fungsi tersebut. Pabrik akan mencapai tujuan produksi asalkan jumlah pekerja (x) adalah antara dua nilai tersebut.
Atur kedua fungsi menjadi sama satu dengan yang lain, dan cari penyelesaian untuk x.
-x2 + 30x = 200
x2 – 30x + 200 = 0
(x – 10)(x – 20) = 0
x = 10 or x = 20
Jadi pabrik akan memproduksi sekurangnya 200 unit selama ada 10 sampai 20 orang pekerja pada suatu waktu.
Tidak ada komentar:
Posting Komentar