Persamaan Lingkaran - Coba kalian perhatikan sepeda yang sering kita jumpai di sekitar kita. Berbentuk apakah permukaan dari roda sepeda itu? Demikian pula berbentuk apakah permukaan dari gir sepeda itu?
Ternyata, bentuk permukaan roda sepeda itu berbentuk lingkaran, demikian juga bentuk permukaan gir sepeda juga berbentuk lingkaran. Tampak bahwa tempat kedudukan dari titik-titik yang berada pada tepi permukaan roda sepeda dan gir itu berjarak sama terhadap titik tertentu. Sekarang, pada topik ini kita mempelajari bidang datar yang berbentuk lingkaran.
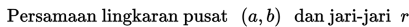
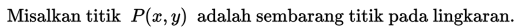

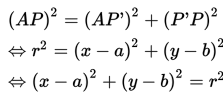
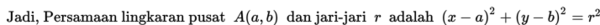
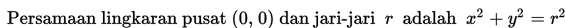
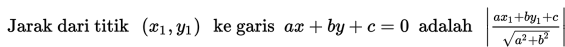
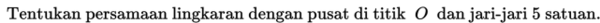
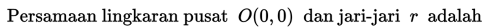
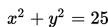
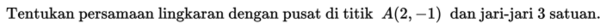
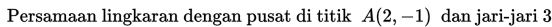
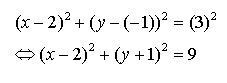
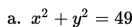
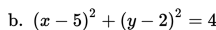
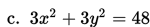
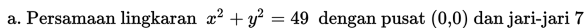
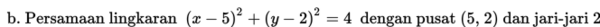
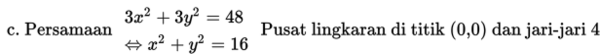
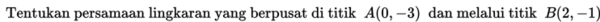
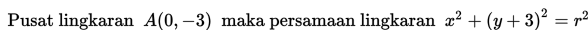
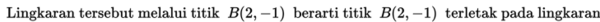
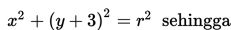
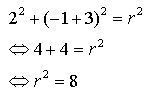
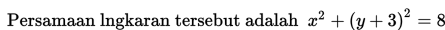
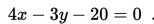
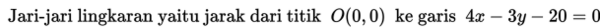


Tentang:
Matematika
 |
| Persamaan Lingkaran |
Ternyata, bentuk permukaan roda sepeda itu berbentuk lingkaran, demikian juga bentuk permukaan gir sepeda juga berbentuk lingkaran. Tampak bahwa tempat kedudukan dari titik-titik yang berada pada tepi permukaan roda sepeda dan gir itu berjarak sama terhadap titik tertentu. Sekarang, pada topik ini kita mempelajari bidang datar yang berbentuk lingkaran.
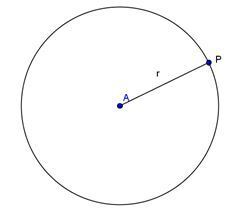
Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama terhadap suatu titik tertentu.
Titik tertentu itu merupakan pusat lingkaran dan jarak yang sama sebagai jari-jari lingkaran.

PERSAMAAN LINGKARAN
Perhatikan gambar berikut ini!


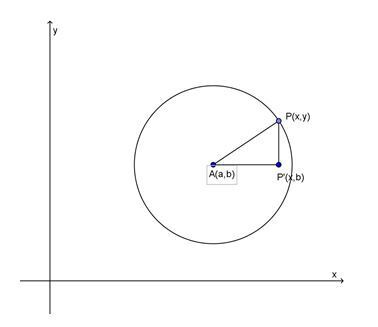
(jar-jari lingkaran) berlaku Teorema Pythagoras
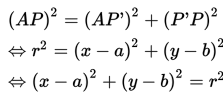
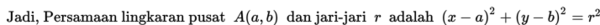
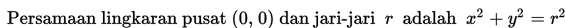
Pusat lingkaran terletak pada titik tengah dari garis tengah (diameter) lingkaran.
Panjang garis tengah (diameter) adalah dua kali panjang jari-jari lingkaran tersebut.
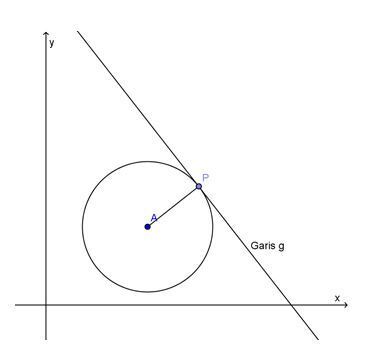
Garis singgung lingkaran memotong lingkaran pada satu titik.
Panjang garis tengah (diameter) adalah dua kali panjang jari-jari lingkaran tersebut.
Garis singgung lingkaran memotong lingkaran pada satu titik.

Garis AP adalah jari-jari lingkaran.
Garis g adalah garis singgung lingkaran. Titik P merupakan titik singgung.
Garis AP tegak lurus dengan garis singgung. Panjang AP adalah jarak dari titik A ke garis g
Garis g adalah garis singgung lingkaran. Titik P merupakan titik singgung.
Garis AP tegak lurus dengan garis singgung. Panjang AP adalah jarak dari titik A ke garis g
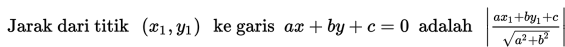
Mari kita cermati beberapa contoh soal berikut ini.
Contoh 1:
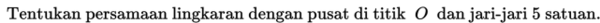
Penyelesaian:
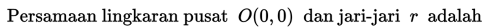
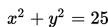
Contoh 2:
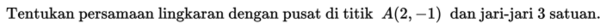
Penyelesaian:
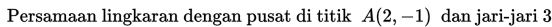
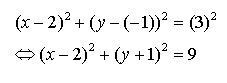
Contoh 3:
Tentukan pusat dan jari-jari lingkaran:
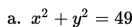
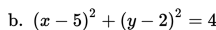
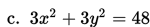
Penyelesaian:
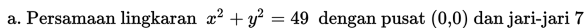
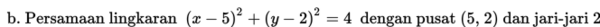
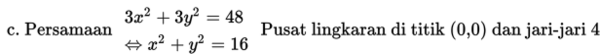
Contoh 4:
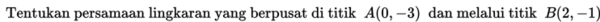
Penyelesaian:
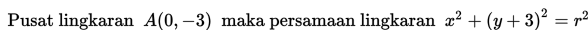
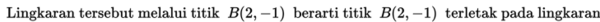
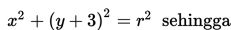
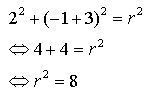
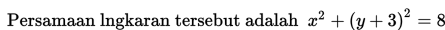
Contoh 5:
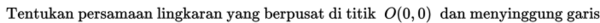
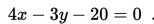
Penyelesaian:
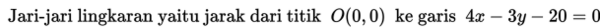


Tidak ada komentar:
Posting Komentar