Sifat Garis Singgung Lingkaran - Dalam mempelajari sifat-sifat garissinggung lingkaran kita juga akan mempelajari tentang pengertian garis singgung pada lingkaran, sifat-sifat garis singgung lingkaran, menentukan panjang garis singgung, dan garis singgung persekutuan dua lingkaran.
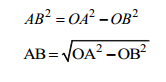
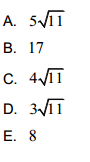
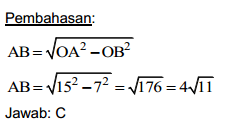

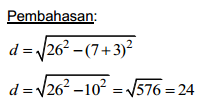


Tentang:
Matematika
 |
| Sifat Garis Singgung Lingkaran |
Marilah kita pelajari satu per satu.
1. Kedudukan garis terhadap lingkaran
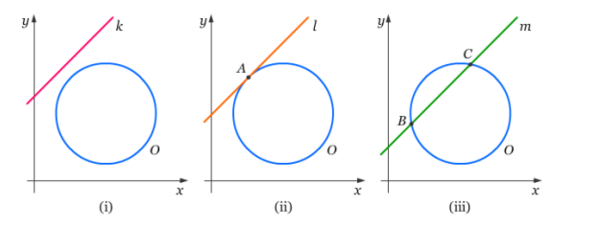
Perhatikan gambar berikut ini yang menunjukan beberapa kedudukan garis terhadap
lingkaran.
lingkaran.

Gambar (i) menunjukkan garis k tidak memotong lingkaran O .
Gambar (ii) menunjukkan garis l menyinggung lingkaran O di titik A.
Gambar (iii) menunjukkan garis m memotong lingkaran O di titik B dan titik C.
Garis singgung lingkaran adalah garis yang memotong suatu lingkaran di satu titik dan berpotongan tegak lurus dengan jari-jari di titik singgungnya.
Gambar (ii) menunjukkan garis l menyinggung lingkaran O di titik A.
Gambar (iii) menunjukkan garis m memotong lingkaran O di titik B dan titik C.
Garis singgung lingkaran adalah garis yang memotong suatu lingkaran di satu titik dan berpotongan tegak lurus dengan jari-jari di titik singgungnya.
2. Sifat-sifat garis singgung lingkaran
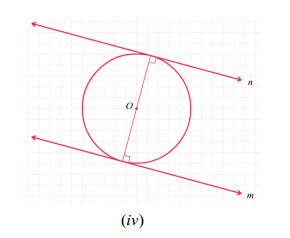
1) Garis singgung lingkaran tegak lurus pada diameter lingkaran yang melalui titik
singgungnya.
singgungnya.

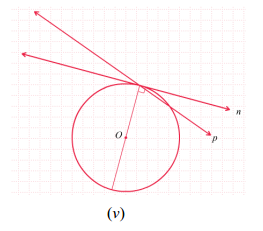
2) Melalui suatu titik pada lingkaran hanya dapat dibuat satu dan hanya satu garis singgung pada lingkaran tersebut.

Garis p bukan garis singgung lingkaran O. Garis n merupakan garis singgung lingkaran O .
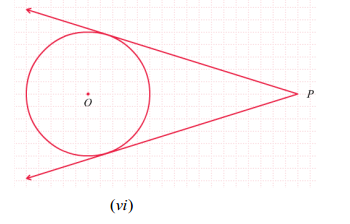
3) Melalui suatu titik di luar lingkaran dapat dibuat dua garis singgung pada lingkaran tersebut.
3) Melalui suatu titik di luar lingkaran dapat dibuat dua garis singgung pada lingkaran tersebut.

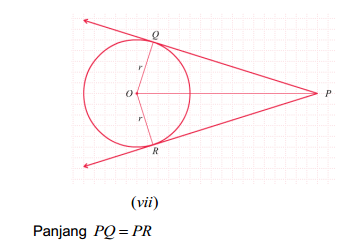
4) Jika P di luar lingkaran maka jarak P ke titik-titik singgungnya adalah sama.

3. Menentukan panjang garis singgung dari suatu titik di luar lingkaran

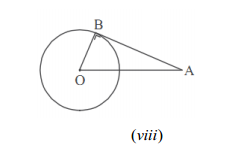
AB adalah garis singgung lingkaran O , AB tegaklurus OB , OB adalah jari-jari lingkaran.
Panjang AB ditentukan dengan menggunakan dalil Pythagoras.
Panjang AB ditentukan dengan menggunakan dalil Pythagoras.
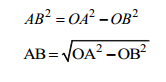
Diketahui sebuah lingkaran dengan pusat di O dan panjang jari-jari 7cm. Garis AB adalah garis singgung lingkaran yang ditarik dari titik A di luar lingkaran. Jika panjang OA 15cm , panjang AB ...cm
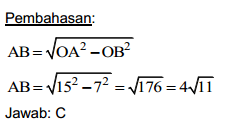
4. Garis Singgung Persekutuan Dua Lingkaran
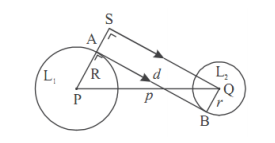
a. Garis Singgung Persekutuan Dalam Dua Lingkaran Diketahui dua lingkaran L1 dan L2 berpusat di P dan Q, dan panjang jari-jari R dan r.
a. Garis Singgung Persekutuan Dalam Dua Lingkaran Diketahui dua lingkaran L1 dan L2 berpusat di P dan Q, dan panjang jari-jari R dan r.

AB adalah garis singgung persekutuan dalam dua lingkaran L1 dan L2. Panjang PQ = p , panjang AB = d.
Cara menentukan panjang AB sebagai berikut.
- Buatlah garis SQ yang sejajar AB dan sama panjang, sehingga terbentuk segitiga siku-siku PQS .
- Panjang AB SQ , tetapkan panjang SQ dengan dalil Pythagoras.
- Buatlah garis SQ yang sejajar AB dan sama panjang, sehingga terbentuk segitiga siku-siku PQS .
- Panjang AB SQ , tetapkan panjang SQ dengan dalil Pythagoras.

Contoh:
Dua lingkaran dengan panjang jari-jari 7 cm dan 3 cm, jarak antara dua titik pusat adalah 26 cm. Panjang garis singgung persekutuan dalam adalah … cm.
A. 24
B. 20
C. 18
D. 16
E. 12
Dua lingkaran dengan panjang jari-jari 7 cm dan 3 cm, jarak antara dua titik pusat adalah 26 cm. Panjang garis singgung persekutuan dalam adalah … cm.
A. 24
B. 20
C. 18
D. 16
E. 12
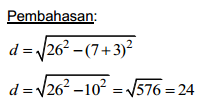
Jadi, Panjang garis singgung persekutuan dalam adalah 24 cm.
Jawab : A
Jawab : A
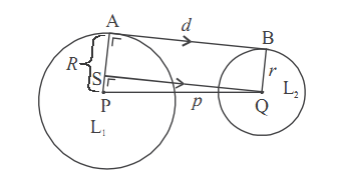
b. Garis Singgung Persekutuan Luar Dua LingkaranDiketahui dua lingkaran L1dan L2berpusat di P dan Q, dan panjang jari-jari R dan r .

AB adalah garis singgung persekutuan luar dua lingkaran L1 dan L2. Panjang PQ = p, panjang AB = d.
Cara menentukan panjang AB sebagai berikut :
- Buatlah garis SQ yang sejajar AB dan sama panjang, sehingga terbentuk segitiga siku-siku PQS.
- Panjang AB = SQ, tetapkan panjang SQ dengan dalil Pythagoras
Cara menentukan panjang AB sebagai berikut :
- Buatlah garis SQ yang sejajar AB dan sama panjang, sehingga terbentuk segitiga siku-siku PQS.
- Panjang AB = SQ, tetapkan panjang SQ dengan dalil Pythagoras

Contoh:
Dua lingkaran dengan panjang jari-jari 8 cm dan 3 cm, jarak antara dua titik pusat
adalah 13 cm. Panjang garis singgung persekutuan luar adalah … cm.
A. 15
B. 12
C. 10
D. 9
E. 7
Dua lingkaran dengan panjang jari-jari 8 cm dan 3 cm, jarak antara dua titik pusat
adalah 13 cm. Panjang garis singgung persekutuan luar adalah … cm.
A. 15
B. 12
C. 10
D. 9
E. 7

Tidak ada komentar:
Posting Komentar