Contoh Soal Pertidaksamaan Pecahan - Pertidaksamaan pecahan adalah adalah pertidaksamaan yang melibatkan persamaan pembilang dan penyebut dengan tanda pertidaksamaan (<, ≤, >, ≥). Pertidaksamaan pecahan ada banyak bentuk dan variasinya.
Contoh :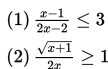
Bagaimanakah bentuk baku dari pertidaksamaan pecahan?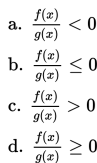
Contoh 1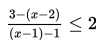
Penyelesaian :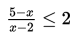
Selanjutnya, kita perlu memindahkan semua elemen pada ruas kanan ke ruas kiri, kemudian menyederhanakannya.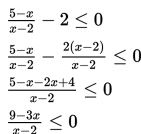
Pembuat nol dari pembilang dan penyebut pada pecahan di atas adalah x = 3 dan x = 2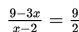
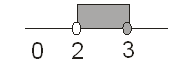
Contoh 2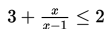
Penyelesaian :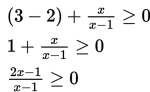
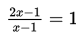
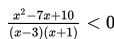
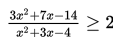
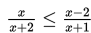
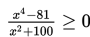
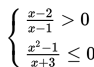
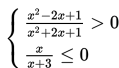

Tentang:
MIA kelas 10
Contoh :
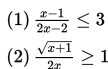
Peridaksamaan (1) adalah contoh pertidaksamaan pecahan yang melibatkan pertidaksamaan linear pada pembilang dan penyebutnya. Adapun pertidaksamaan (2) adalah pertidaksamaan pecahan yang melibatkan pertidaksamaan irrasional.
Bagaimanakah bentuk baku dari pertidaksamaan pecahan?
Ada 4 bentuk baku dari pertidaksamaan pecahan, yaitu :
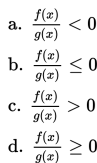
dengan syarat g(x) ≠ 0
Contoh 1
Tentukan himpunan penyelesaian dari
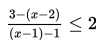
Penyelesaian :
Yang perlu dilakukan adalah menyederhanakan ruas kiri terlebih dahulu, sehingga diperoleh hasil sebagai berikut :
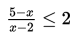
Selanjutnya, kita perlu memindahkan semua elemen pada ruas kanan ke ruas kiri, kemudian menyederhanakannya.
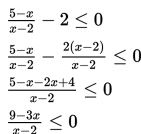
Pembuat nol dari pembilang dan penyebut pada pecahan di atas adalah x = 3 dan x = 2
Langkah selanjutnya adalah melakukan uji titik. Misal diambil x = 0 sebagai titik uji, maka diperoleh :
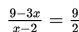
Karena untuk x = 0 diperoleh hasil positif, maka daerah pada x < 2 bernilai positif, daerah pada interval 2 < x ≤ 3 bernilai negatif, dan daerah pada x > 3 bernilai positif.
Jadi, himpunan penyelesaian pertidaksamaan di atas adalah {x ∈ ℝ | 2 < x ≤ 3}
Untuk lebih jelasnya, mari perhatikan daerah arsiran pada garis bilangan berikut ini :
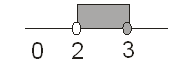
Ingat, x = 2 bukan penyelesaian karena merupakan pembuat nol dari penyebut.
Contoh 2
Tentukan himpunan penyelesaian dari
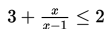
Penyelesaian :
Yang perlu dilakukan adalah memindahkan semua elemen di ruas kanan ke ruas kiri terlebih dahulu, sehingga diperoleh hasil sebagai berikut :
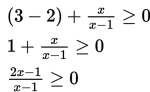
Pembuat nol dari pembilang dan penyebut dari pecahan di atas adalah x = 1/2 dan x = 1
Langkah selanjutnya adalah melakukan uji titik. Misal diambil x = 0 sebagai titik uji, maka diperoleh :
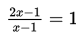
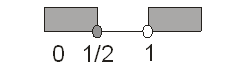
Karena untuk x = 0 diperoleh hasil positif, maka daerah pada x ≤ ½ bernilai positif, daerah pada interval ½ ≤ x < 1 bernilai negatif, dan daerah pada x > 1 bernilai positif.
Jadi, himpunan penyelesaian pertidaksamaan di atas adalah {x ∈ ℝ | x ≤ ½ atau x > 1}
Untuk lebih jelasnya, mari perhatikan daerah arsiran pada garis bilangan berikut ini :

Ingat, x = 1 bukan penyelesaian karena merupakan pembuat nol penyebut.
S1
Himpunan penyelesaian dari
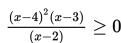
adalah..
S2
Himpunan penyelesaian dari
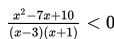
adalah..
S3
Himpunan penyelesaian dari
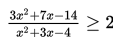
adalah...
S4
Himpunan penyelesaian dari
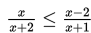
adalah...
S5
Himpunan penyelesaian dari
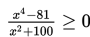
adalah...
S6
Himpunan penyelesaian dari
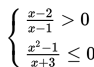
adalah...
S7
Himpunan penyelesaian dari
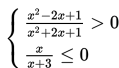
adalah...
S8
Himpunan penyelesaian dari

adalah...
S9
Diberikan pertidaksamaan
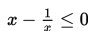
adalah...
S10
Himpunan penyelesaian dari
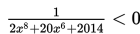
adalah...

Tidak ada komentar:
Posting Komentar