Contoh Soal Model Matematika Sistem Pertidaksamaan Kuadrat Dua Variabel - Pada topik sebelumnya kita telah mempelajari konsep pertidaksamaan kuadrat dua variabel. Dalam topik ini kita akan mempelajari model matematika sistem pertidaksamaan kuadrat dua variabel.
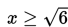
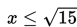
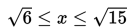
Tentang:
MIA kelas 10
Sebelum kita memulai topik model matematika sistem pertidaksamaan kuadrat dua variabel, marilah kita mengingat kembali konsep dari sistem pertidaksamaan kuadrat dua variabel.
Sistem Pertidaksamaan kuadrat dua variabel
Pertidaksamaan kuadrat dua variabel merupakan pertidaksamaan yang memuat dua variabel dengan pangkat tertinggi dua.
Contoh bentuk umum pertidaksamaan kaudrat dua variabel
Pertidaksamaan kuadrat dua variabel merupakan pertidaksamaan yang memuat dua variabel dengan pangkat tertinggi dua.
Contoh bentuk umum pertidaksamaan kaudrat dua variabel
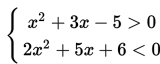
Apakah kalian sudah ingat kembali? Jika sudah, mari kita pelajari model matematika sistem Pertidaksamaan kuadrat dua variabel
Model Matematika Sistem Pertidaksamaan Kuadrat Dua Variabel
Langkah – langkah dalam menyelesaikan model matematika sistem pertidaksamaan kuadrat dua variabel yaitu :
1. Mencari kata – kata seperti “ kurang dari”(<), “lebih dari”(>), “tidak lebih dari”(≤), tidak kurang dari”(≥).
2. Setelah menemukan kata – kata tersebut merumuskan model matematika dari masalah
3. Menentukan penyelesaian dari model matematika
4. Memberikan penafsiran dari hasil yang didapat
Agar lebih memahami marilah kita mencermati contoh dibawah ini
Contoh:
Panjang dan lebar dari persegi panjang ABCD masing – masing 30 cm dan 20 cm bagian tepi persegi panjang tersebut dipotong selebar x2 sehingga diperoleh persegi panjang PQRS. Jika keliling persegi panjang PQRS tidak kurang dari 52 cm maka tentukan batas – batas x yang dapat dilakukan.
Penyelesaian:
Misal panjang persegi panjang PQRS = 30- 2x2 , lebar persegi panjang PQRS = 20 – 2x2
Keliling persegi panjang PQRS ≤ 52
2( p + l) ≤ 52
2(30 – 2x2 + 20 -2x2 ) ≤ 52
2( 50 – 4x2 ) ≤ 52
100 – 8x2 ≤ 52
-8x2 ≤ 52 -100
8x2 ≥ 48
x2 ≥ 6
1. Mencari kata – kata seperti “ kurang dari”(<), “lebih dari”(>), “tidak lebih dari”(≤), tidak kurang dari”(≥).
2. Setelah menemukan kata – kata tersebut merumuskan model matematika dari masalah
3. Menentukan penyelesaian dari model matematika
4. Memberikan penafsiran dari hasil yang didapat
Agar lebih memahami marilah kita mencermati contoh dibawah ini
Contoh:
Panjang dan lebar dari persegi panjang ABCD masing – masing 30 cm dan 20 cm bagian tepi persegi panjang tersebut dipotong selebar x2 sehingga diperoleh persegi panjang PQRS. Jika keliling persegi panjang PQRS tidak kurang dari 52 cm maka tentukan batas – batas x yang dapat dilakukan.
Penyelesaian:
Misal panjang persegi panjang PQRS = 30- 2x2 , lebar persegi panjang PQRS = 20 – 2x2
Keliling persegi panjang PQRS ≤ 52
2( p + l) ≤ 52
2(30 – 2x2 + 20 -2x2 ) ≤ 52
2( 50 – 4x2 ) ≤ 52
100 – 8x2 ≤ 52
-8x2 ≤ 52 -100
8x2 ≥ 48
x2 ≥ 6
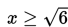
Panjang persegi panjang PQRS ≥ 0
30 – 2x2 ≥ 0
-2x2 ≥ - 30
2x2 ≤ 30
x2 ≤ 15
30 – 2x2 ≥ 0
-2x2 ≥ - 30
2x2 ≤ 30
x2 ≤ 15
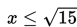
Batas – batas yang dapat dilakukan
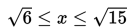
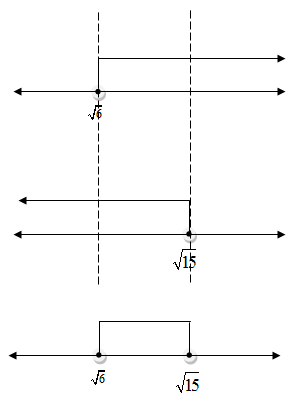
S1
Suatu persegi panjang dengan panjang a cm dan lebarnya (a - 5) cm. Luas persegi panjang kurang dari 6 cm2 dan panjang diagonalnya lebih dari 5 cm. Batas nilai a yang memenuhi adalah ….
S2
Alas sebuah segitiga sama kaki adalah t – 3, sisi yang lain adalah t dan tingginya adalah t. Luas segitiga sama kaki tersebut kurang dari 27 cm dan kelilingnya tidak kurang dari 9 cm. Batas nilai t yang mungkin adalah ….
S3
Ada dua bilangan dimana bilangan pertama adalah x + 1 sedangkan bilangan kedua adalah x + 2. Hasil perkalian lebih dari 30 dan perjumlahan kuadratnya lebih dari 41. Nilai batas x yang mungkin adalah ….
S4
Segitiga siku – siku dengan alas (a – 1) cm, tinggi a cm dan sisi miring (2a -1) cm. Jika luasnya tidak lebih dari 6 cm dan sisi miringnya lebih dari 11 cm maka batas nilai a yang memenuhi adalah .…
S5
Suatu pekarangan rumah berbentuk persegi panjang dengan panjang x dan lebarnya x +1 jika kelilingnya lebih dari 14 cm dan luasnya kurang dari 20 cm2 maka tentukan batas – batas x yang memenuhi
S6
Diketahui tiga buah bilangan berurutan x, y, dan z. Hasil kali bilangan kedua dan bilangan ketiga lebih dari 20 sedangkan hasil kali bilangan pertama dan kedua lebih dari 12. Batas – batas bilangan tersebut yang mungkin adalah ….
S7
Panjang dan lebar suatu persegi panjang adalah (x + 1) cm. Bila panjangnya ditambah 3 cm dan lebarnya ditambah 1 cm maka luasnya menjadi lebih besar dari 35 cm2 sedangkan apabila panjang dikurangi 2 cm dan lebarnya dikurangi 1cm luasnya menjadi lebih kecil dari 72 cm2. Batas nilai x agar menjadi ukuran maksimum adalah ….
S8
Panjang dan lebar dari persegi panjang ABCD masing – masing 20 cm dan 10 cm bagian tepi persegi panjang tersebut dipotong selebar 2x2 sehingga diperoleh persegi panjang PQRS. Keliling persegi panjang PQRS tidak kurang dari 12. Batas nilai x yang memenuhi adalah ….
S9
Selisih kuadrat suatu bilangan dengan tiga kali bilangan itu kurang dari 25 sedangkan jumlah kuadrat bilangan itu dengan lima kali bilangan tersebut lebih dari 9. Batas nilai bilangan itu adalah….
S10
Kuadrat suatu bilangan tidak lebih dari bilangan itu sendiri. Sedangkan selisih kuadrat bilangan itu dengan 3 kali bilangan tersebut tidak lebih dari 4. Batas bilangan itu adalah ….

Tidak ada komentar:
Posting Komentar