Contoh Soal Persamaan Eksponen Berbentuk a^f(x) = b^f(x) - Pada topik terdahulu, kalian telah mempelajari persamaan eksponen berbentuk af (x) = 1 dan af (x) = ap. Dalam topik ini, kita akan memahami suatu materi yang masih berkaitan dengan materi persamaan eksponen yaitu persamaan eksponen berbentuk af (x) = bf (x). Cara penentuan himpunan penyelesaian suatu persamaan eksponen berbeda-beda tergantung bentuk persamaannya. Persamaan eksponen berbentuk af (x) = bf (x) memiliki keunikan dibandingkan dengan persamaan eksponen yang telah dibahas sebelumnya. Keunikannya yaitu pada kedua ruas persamaan, eksponennya berupa fungsi dalam x yang persis sama, sedangkan bilangan pokoknya berbeda. Hal ini tentunya berbeda dari materi sebelumnya dimana pangkat eksponennya berupa bilangan (konstanta) pada salah satu ruas dengan bilangan pokok yang sama.
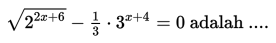
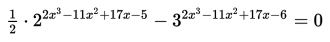
Tentang:
Matematika Ipa kelas 12
Untuk memudahkan kalian dalam menentukan himpunan penyelesaian dari persamaan eksponen berbentuk af (x) = bf (x), mari kita ingat kembali penyelesaian dari beberapa contoh soal yang berkaitan dengan persamaan eksponen berbentuk af (x) = 1 dan af (x) = ap.
SOAL 1
Himpunan penyelesaian dari persamaan 25x - 2 = 45x - 2 adalah ....
SOAL 2
Nilai x yang memenuhi persamaan . (5)x = 4x - 2adalah ....
SOAL 3
Himpunan penyelesaian dari persamaan 2x2 – 1 = 5x2 – 1 adalah ....
SOAL 4
Himpunan penyelesaian yang memenuhi persamaan 8. 23x - 5 - 33x - 2 = 0 adalah ....
SOAL 5
Nilai x yang memenuhi persamaan:
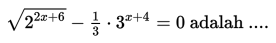
SOAL 6
Akar-akar penyelesaian dari persamaan 3x2 - x - 2 = 8x2 - x - 2 adalah x1 dan x2. Jika x1 > x2 maka nilai dari 4x1 - 2x2 adalah ....
SOAL 7
Jika x1 dan x2 memenuhi persamaan 92x2 – 5x + 3 = 102x2 – 5x + 3 , maka nilai dari x1 + x2 adalah ....
SOAL 8
Himpunan penyelesaian dari persamaan 3x3 + 2x2 – 5x - 6 = 5x3 + 2x2 – 5x - 6 adalah ....
SOAL 9
Himpunan penyelesaian dari persamaan 22x3 + 7x2 - 10x - 24 = 52x3 + 7x2 - 10x - 24adalah ....
SOAL 10
Akar-akar penyelesaian dari persamaan eksponen:
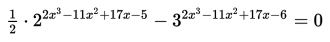
adalah x1, x2, dan x3. Jika x1 < x2 < x3, maka nilai dari 2x1 + x2 - x3 adalah ....

Tidak ada komentar:
Posting Komentar