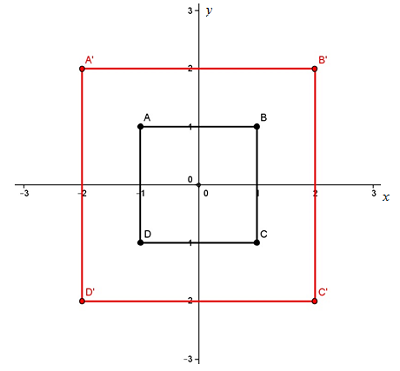
Contoh Soal Dilatasi - Dalam ilmu matematika, dilatasi juga diartikan sebagai perubahan suatu ukuran benda---diperbesar atau diperkecil---yang tidak mengubah bentuk asalnya. Faktor yang menyebabkan diperbesar atau diperkecilnya suatu benda ini disebut dengan faktor skala dilatasi. Agar kamu lebih paham tentang dilatasi dan faktor skalanya, perhatikan gambar persegi ABCD dan A’B’C’D’ berikut ini.
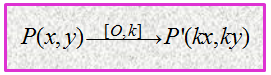
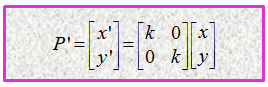
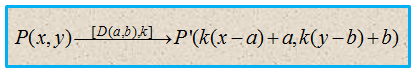
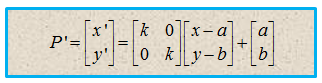
Tentang:
Index
Matematika Ipa kelas 12

Pada gambar di atas, dapat diketahui bahwa bentuk persegi ABCD dan persegi A’B’C’D’ adalah sama. Namun, ukurannya berbeda. Hubungan antara persegi ABCD dan persegi A’B’C’D’ dapat kamu pahami dari penjelasan berikut.
Persegi A’B’C’D’ memiliki panjang sisi 2 kali panjang sisi persegi ABCD. Sebaliknya, persegi ABCD memiliki panjang sisi kali panjang sisi persegi A’B’C’D’. Dengan demikian, dapat dikatakan bahwa persegi A’B’C’D’ merupakan hasil dilatasi diperbesar dari persegi ABCD terhadap pusat dilatasi titik asal O(0, 0) dengan faktor skala dilatasi 2, sedangkan persegi ABCD merupakan hasil dilatasi diperkecil dari persegi A’B’C’D’ terhadap pusat dilatasi titik asal O(0, 0) dengan faktor skala dilatasi .
Dari penjelasan di atas, dapat diketahui bahwa faktor skala dilatasi menentukan apakah suatu objek mengalami pengecilan atau perbesaran. Jika bilangan real k menyatakan faktor skala dilatasi, maka:
☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳
📌 untuk k < -1 atau k > 1, bayangan diperbesar;
📌 untuk k = 1, bayangan tidak mengalami perubahan; dan
📌 untuk -1 < k < 1, bayangan diperkecil.
☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳
Seperti halnya dengan jenis transformasi lainnya, dilatasi juga mempunyai matriks transformasi yang sesuai untuk menyatakan proses dilatasi. Perhatikan ilustrasi di bawah ini.

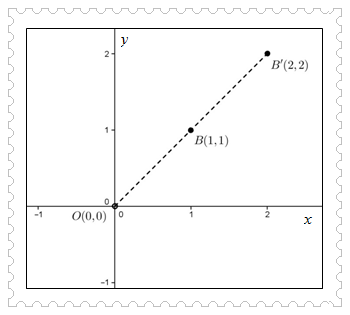
Titik B(1, 1) didilatasi terhadap titik asal 0(0, 0) dengan faktor skala 2 menghasilkan bayangan berupa titik B’(2, 2). Matriks dilatasi yang sesuai untuk dilatasi titik B adalah sebagai berikut.
Sebaliknya, kita juga dapat memandang titik B’(2, 2) didilatasi terhadap titik asal 0(0, 0) dengan faktor skala menghasilkan bayangan berupa titik B(1, 1). Matriks dilatasi yang sesuai untuk dilatasi titik B’ adalah sebagai berikut.
Dari uraian di atas, dilatasi titik P(x, y) terhadap titik asal O(0, 0) dengan faktor skala k, secara umum akan menghasilkan bayangan berupa titik P’(kx, ky).
Dalam notasi transformasi, dilatasi ini dituliskan sebagai:
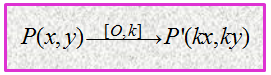
Dalam notasi matriks, dilatasi ini dituliskan sebagai:
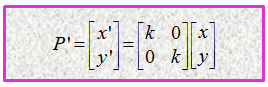
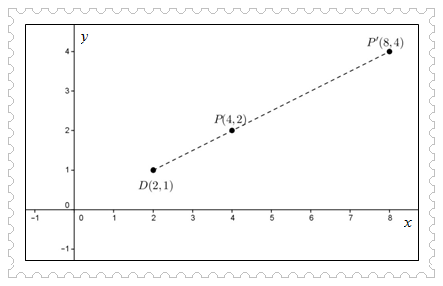
Pertanyaan selanjutnya yang muncul adalah bagaimana jika dilatasi tidak berpusat di titik O(0, 0)? Notasi matriks seperti apa yang sesuai untuk menyatakannya? Untuk tahu jawabannya, perhatikan ilustrasi di bawah ini ya.

Titik P(4, 2) didilatasi terhadap titik D(2, 1) dengan faktor skala 3 menghasilkan bayangan berupa titik P’(8, 4). Matriks dilatasi yang sesuai untuk dilatasi titik P adalah:
Sebaliknya, kita juga dapat memandang titik P’(8, 4) didilatasi terhadap titik D(2, 1) dengan faktor skala menghasilkan bayangan berupa titik P(4, 2). Matriks dilatasi yang sesuai untuk dilatasi titik P’ adalah:
Dari uraian di atas, dilatasi titik P(x, y) terhadap pusat dilatasi titik D(a, b) dengan faktor skala k, secara umum akan menghasilkan bayangan berupa titik P’(k (x - a) + a, k(y - b) + b).
Dalam notasi transformasi, dilatasi ini dituliskan sebagai:
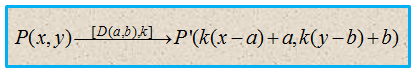
Dalam notasi matriks, dilatasi ini dituliskan sebagai:
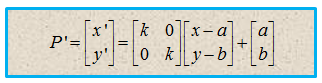
☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳
💻 Sifat Dilatasi
📍 Bayangan sebuah titik hasil dilatasi selalu segaris (kolinear) dengan titik pusat dilatasi dan titik yang didilatasikan.
📍 Dilatasi dengan skala k ≠ 0 pada objek geometri tidak mengubah karakteristik dari objek tersebut, namun hanya mengubah ukurannya saja.
SOAL 1
Titik A dan B terpisah sejauh 3 satuan. Titik C berada tepat ditengah kedua titik tersebut. Apabila A dan B didilatasi dengan faktor skala 2 terhadap titik C, jarak pisah bayangan A dan B adalah ….
SOAL 2
Persegi ABCD memiliki luas 4 satuan. Apabila persegi tersebut didilatasi dengan faktor skala 2 terhadap titik perpotongan diagonalnya, maka luas bangun hasil dilatasi persegi tersebut adalah ….
SOAL 3
Bayangan titik A(7, 2) setelah didilatasi dengan faktor skala 3 terhadap titik asal O(0, 0) adalah ….
SOAL 4
Bayangan titik B(6, 9) setelah didilatasi dengan faktor skala terhadap titik asal O(0, 0) adalah ….
SOAL 5
Titik A(4, 2) didilatasi dengan faktor skala 5 terhadap titik D(3, 1). Bayangan dari dilatasi tersebut adalah ….
SOAL 6
Titik B(-4, 6) didilatasi dengan faktor skala terhadap titik D(1, -4). Bayangan dari dilatasi tersebut adalah ….
SOAL 7
Bayangan dari titik P(2, 1) setelah didilatasi terhadap titik asal O(0, 0) adalah P’(14, 7). Faktor skala yang digunakan dalam dilatasi tersebut adalah ….
SOAL 8
Bayangan titik Q(4, -2) setelah didilatasi terhadap titik D(-4, 2) adalah Q’(2, -1). Faktor skala yang digunakan dalam dilatasi tersebut adalah ….
SOAL 9
Sebuah lingkaran l dengan jari-jari 2 satuan didilatasi dengan faktor skala terhadap titik pusat lingkaran tersebut. Perbandingan luas lingkaran hasil dilatasi dengan lingkaran awalnya adalah….
SOAL 10
Sebuah kubus satuan ABCD.EFGH didilatasi dengan faktor skala 3 terhadap titik hasil perpotongan diagonalnya. Perbandingan luas permukaan kubus dengan bayangannya adalah ….

Tidak ada komentar:
Posting Komentar