Contoh Soal Menafsirkan bentuk aljabar rumit - Sebagian besar dari polinomial yang akan kalian hadapi adalah dalam bentuk
1 x 2 − 3 x − 4 ) − 2 x 2 − 3 x − 4 ) 2 ,Karena fungsinya diarahkan kepada eksponen negatif, kalian dapat membalikkan pembilang dan penyebutnya serta menghilangkan bentuk negatif dari eksponen
1 3 x 2 − 2 x + 7 ) − 2 I ) [ ( 3.3 ) 2 x 1 3 + 7.1 ( ( x ) 4 ) 1 2 + ( − 9 ) = 0 ] ( I I ) [ ( 8.4 2 ) x + 101.99 x = 77 4 ] ( I I I ) [ x − 1 + 2 = 0 ]
5 3 + x 2 + ( 49 ) 1 2 x − x 3 = 7 x x 2 + ( − 3 x ) 3 x 6
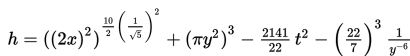
A ) [ ( 3 x 2 ) a 2 + 7 x + 9 = 33 x 4 ] ( B ) [ 2 x 3 + Π 3 x 4 = − 9 ] ( C ) [ 8 x 5 = 0 ]
Tentang:
MIA kelas 11
sederhana yang dapat kalian kenali, seperti
x2+7x+10. Polinomial ini memiliki tiga suku, yang membuatnya menjadi sebuah trinomial. Koefisen-koefisiennya juga mudah untuk ditentukan; koefisien pada x2 adalah satu dan tujuh pada x. Kalian bahkan bisa lebih jauh membahasnya dan memfaktorkan polinomialnya menjadi (x+5)(x+2), memisahkan faktor-faktor kalian.
x2+7x+10. Polinomial ini memiliki tiga suku, yang membuatnya menjadi sebuah trinomial. Koefisen-koefisiennya juga mudah untuk ditentukan; koefisien pada x2 adalah satu dan tujuh pada x. Kalian bahkan bisa lebih jauh membahasnya dan memfaktorkan polinomialnya menjadi (x+5)(x+2), memisahkan faktor-faktor kalian.
Namun ada beberapa polinomial seperti 1 x 2 − 3 x − 4 ) − 2
Berapa derajat fungsi ini? Polinomial jenis apa ini? Pertanyaan-pertanyaan ini tampaknya sulit, tapi jika kalian belajar bagaimana cara untuk menginterpretrasikan ekspresi/bentuk rumit, prosesnya akan menjadi jauh lebih mudah. Sekarang mari kita coba menjawab pertanyaan-pertanyaan tersebut:
x2-3x-4, Jika kalian memangkatkan suatu bilangan yang sedang di-akar pangkat-kan, maka operasinya akan batal/dihapus
Sekarang kita dapat melihat bahwa polinomial ini adalah sebuah trinomial derajat-kedua. Ini dapat difaktorkan menjadi (x-4)(x+1). Tidak begitu sulit kan? Kuncinya adalah harus tetap sabar karena bentuk/ekspresi rumit ini seringkali membutuhkan beberapa langkah untuk menyederhanakannya menjadi bentuk-bentuk yang lebih sederhana.
Permasalahan
lainnya yang seringkali dihadapi oleh para siswa adalah konstanta yang ditulis sebagai huruf karena para siswa tidak yakin tentang berapa banyak suku di dalam polinomial. Contoh, mari tetapkan T=3. Jika
kemudian kalian melihat persamaan y=Tx, kalian akan bingung. Berapa variabelnya, T, x, atau keduanya? Namun ingat, bahwa T=3, dan persamaannya dapat ditulis sebagai y=3x, jadi hanya ada satu suku, satu variabel, dan koefisiennya adalah T atau 3.
lainnya yang seringkali dihadapi oleh para siswa adalah konstanta yang ditulis sebagai huruf karena para siswa tidak yakin tentang berapa banyak suku di dalam polinomial. Contoh, mari tetapkan T=3. Jika
kemudian kalian melihat persamaan y=Tx, kalian akan bingung. Berapa variabelnya, T, x, atau keduanya? Namun ingat, bahwa T=3, dan persamaannya dapat ditulis sebagai y=3x, jadi hanya ada satu suku, satu variabel, dan koefisiennya adalah T atau 3.
Mari lihat satu contoh lagi:
Contoh Akhir:
Tipe berapa polinomial dari 1 3 x 2 − 7 x − 2 ) − 2 + 4 x 3 = x 3 / 2 − 49 x 2 + 27 x 6 3
Polinomial ini mungkin kelihatannya sangat membingungkan, tapi jika kita mengerjakannya satu persatu, akan menjadi jauh lebih mudah diselesaikan.
Langkah Pertama: 1 3 x 2 − 7 x − 2 ) − 2 3 x 2 − 7 x − 2 ) x 2 − 7 x − 2 , Hapus pangkat dan akar pangkat, menghasilkan bentuk yang lebih sederhana
Langkah Kedua: x 3 = 2, Jadi kalian dapat menulisnya ulang sebagai 2 x 3 3 sebagai 3 / 2 x 3 / 2
Langkah Ketiga: x 2 Ini dapat menjadi proses langkah tunggal, = 7 dan 2 = x, jadi ini dapat ditulis ulang sebagai 7x
Langkah Empat: x 9 3 Proses satu langkah lagi, 3 = 3 dan 6 3 = x 2 x 2
Langkah Lima: Sekarang mari lihat apa yang kita miliki: ( 3 x 2 − 7 x − 2 ) + x 3 / 2 ) = x 3 / 2 ) – (7x) + ( 3 x 2 )
Langkah Enam: Hapus! ( 3 x 2 − 7 x − 2 ) + x 3 / 2 ) = x 3 / 2 ) – (7x) + ( 3 x 2 )
S1
Berapa banyak suku bilangan dari bentuk berikut?
S2
Mewakili jenis polinomial apakah bentuk berikut?
S3
Berapakah derajat dari bentuk polinomial berikut?
S4
Persamaan berikut menggambarkan Hukum Ohm dalam sirkuit elektronik. Jika diasumsikan bahwa hambatan (R)nya konstan, maka voltase (v)-nya bergantung pada variabel mana?
S5
Manakah pernyataan yang benar mengenai bentuk berikut?
Manakah persamaan yang mempunyai polinomial berderajat sama?
S7
Sederhanakan bentuk berikut.
((1919/2 )(1919/2 - 1))+ (1919 - 2) - (1919/4 - 3)
S8
Polinomial jenis apakah bentuk aljabar berikut?
S9
Jika π = 22 / 7, maka variabel bebas dari fungsi berikut ini adalah ….
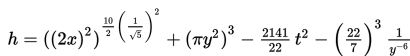
S10
Apa yang bisa kamu katakan tentang polinomial berikut?
(Di sini dianggap bahwa a2= -1 )

Tidak ada komentar:
Posting Komentar