Contoh Soal Merumuskan Fungsi Distribusi Binomial Melalui Percobaan Acak - Di kelas X, tentunya kalian telah mempelajari cara mengumpulkan data. Pengumpulan data dilakukan dengan cara mengambil semua subjek penelitian yang disebut sebagai populasi.
Mari kita perhatikan ilustrasi berikut ini.
Adi ingin mengetahui sejauh mana motivasi belajar teman-temannya di SMA dalam mempelajari matematika. Berkaitan dengan tujuan tersebut, Adi melakukan wawancara dengan setiap siswa di sekolahnya. Setelah beberapa teman di wawancara, Adi sadar bahwa proses wawancara dengan semua siswa di sekolah tentunya akan memakan banyak waktu dan tenaga. Adi kemudian bertanya-tanya tentang ada tidaknya cara yang lebih efisien. Setelah berfikir cukup lama, Adi akhirnya memutuskan untuk mewawancari 2 siswa dari tiap kelas sehingga ada 30 siswa yang mewakili satu sekolah.
Dalam ilustrasi di atas, siswa yang mewakili diharapkan memberikan gambaran yang sesuai dengan sifat populasi. Cara pengambilan data seperti di atas disebut teknik sampling, yaitu pengambilan data yang dilakukan pada sampel kemudian kesimpulannya digeneralisasikan terhadap populasi.
Setelah mengetahui perbedaan populasi dan sampel, kita akan mempelajari distribusi binomial. Pernahkah kalian melakukan suatu percobaan?
Sebuah percobaan memiliki dua kemungkinan, yaitu “berhasil” atau “gagal”. Misalkan kita akan membeli sebuah jeruk. Saat memilih jeruk tersebut, kita dihadapkan pada dua kemungkinan, yaitu manis dan asam. Kita dianggap berhasil memilih jeruk yang bagus ketika kita mengambil jeruk yang manis. Namun jika kita mengambil jeruk yang asam, maka kita dianggap gagal dalam memilih jeruk yang bagus. Jika setiap jeruk yang diambil dikembalikan ke dalam keranjang sebelum pengambilan berikutnya, maka percobaan yang baru memiliki sifat yang sama, yaitu perulangannya bersifat bebas dan peluang terambilnya jeruk yang manis selalu sama, yaitu ½.
Percobaan seperti pada contoh di atas disebut percobaan binomial. Distribusi binomial adalah suatu distribusi probabilitas yang dapat digunakan apabila suatu proses dan cara pengambilan sampel dapat diasumsikan sesuai dengan proses Bernoulli.
Mari kita perhatikan percobaan binomial berikut!
Sebuah jeruk diambil dari sebuah keranjang yang berisi 30 jeruk manis (M) dan 70 jeruk asam (A). Percobaan dikatakan berhasil jika jeruk yang terambil adalah jeruk yang manis. Misal, banyaknya keberhasilan dilambangkan dengan variabel acak x dengan nilai sebagai berikut :
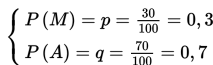
Contoh 1 :
Contoh 2 :
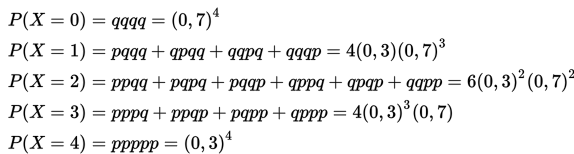
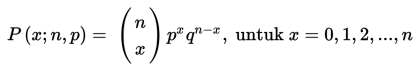
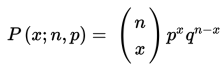

Tentang:
MIA kelas 11
Mari kita perhatikan ilustrasi berikut ini.
Adi ingin mengetahui sejauh mana motivasi belajar teman-temannya di SMA dalam mempelajari matematika. Berkaitan dengan tujuan tersebut, Adi melakukan wawancara dengan setiap siswa di sekolahnya. Setelah beberapa teman di wawancara, Adi sadar bahwa proses wawancara dengan semua siswa di sekolah tentunya akan memakan banyak waktu dan tenaga. Adi kemudian bertanya-tanya tentang ada tidaknya cara yang lebih efisien. Setelah berfikir cukup lama, Adi akhirnya memutuskan untuk mewawancari 2 siswa dari tiap kelas sehingga ada 30 siswa yang mewakili satu sekolah.
Dalam ilustrasi di atas, siswa yang mewakili diharapkan memberikan gambaran yang sesuai dengan sifat populasi. Cara pengambilan data seperti di atas disebut teknik sampling, yaitu pengambilan data yang dilakukan pada sampel kemudian kesimpulannya digeneralisasikan terhadap populasi.
Setelah mengetahui perbedaan populasi dan sampel, kita akan mempelajari distribusi binomial. Pernahkah kalian melakukan suatu percobaan?
Sebuah percobaan memiliki dua kemungkinan, yaitu “berhasil” atau “gagal”. Misalkan kita akan membeli sebuah jeruk. Saat memilih jeruk tersebut, kita dihadapkan pada dua kemungkinan, yaitu manis dan asam. Kita dianggap berhasil memilih jeruk yang bagus ketika kita mengambil jeruk yang manis. Namun jika kita mengambil jeruk yang asam, maka kita dianggap gagal dalam memilih jeruk yang bagus. Jika setiap jeruk yang diambil dikembalikan ke dalam keranjang sebelum pengambilan berikutnya, maka percobaan yang baru memiliki sifat yang sama, yaitu perulangannya bersifat bebas dan peluang terambilnya jeruk yang manis selalu sama, yaitu ½.
Percobaan seperti pada contoh di atas disebut percobaan binomial. Distribusi binomial adalah suatu distribusi probabilitas yang dapat digunakan apabila suatu proses dan cara pengambilan sampel dapat diasumsikan sesuai dengan proses Bernoulli.
Menurut Walpole, suatu percobaan disebut sebagai percobaan binomial (proses Bernoulli) jika memiliki sifat-sifat berikut :
- Percobaan terdiri dari n ulangan
- Pada setiap pengulangan, hasilnya dapat dinyatakan sebagai berhasil atau gagal
- Peluang berhasil dinyatakan sebagai p sedangkan peluang setiap kegagalan yang terjadi adalah q = 1 – p. Keberhasilan dan kegagalan memiliki peluang yang sama pada setiap pengulangan percobaan
- Pengulangan bersifat bebas satu sama lain. Artinya percobaan pertama tidak mempengaruhi percobaan kedua dan sebaliknya.
Mari kita perhatikan percobaan binomial berikut!
Sebuah jeruk diambil dari sebuah keranjang yang berisi 30 jeruk manis (M) dan 70 jeruk asam (A). Percobaan dikatakan berhasil jika jeruk yang terambil adalah jeruk yang manis. Misal, banyaknya keberhasilan dilambangkan dengan variabel acak x dengan nilai sebagai berikut :

Peluang terambilnya jeruk manis dan jeruk asam berturut-turut adalah
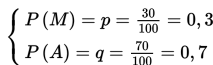
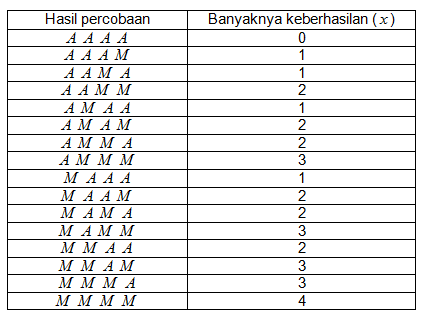
Selanjutnya, jika dimisalkan percobaan dilakukan sebanyak empat kali dan jeruk yang telah diambil pada pengambilan sebelumnya dikembalikan lagi, maka percobaan ini menghasilkan 24 = 16 hasil percobaan sebagai berikut :

Oleh karena setiap hasil percobaan terdiri dari empat kejadian yang bebas satu sama lain, maka peluang terjadinya setiap percobaan merupakan hasil kali peluang setiap kejadian.
Contoh 1 :
Dalam kasus di atas, akan kita tentukan peluang terambil jeruk pertama manis, jeruk ke-2 asam, jeruk ke-3 asam, dan jeruk ke-4 manis.

Contoh 2 :
Jika kita tidak memperhatikan urutan pengambilan jeruk manis dan asam pada contoh 1, maka peluang terambil 1 jeruk manis dan 3 jeruk asam dari 4 kali percobaan adalah

Berdasarkan percobaan di atas, dapat ditunjukkan bahwa jika percobaan dilakukan sebanyak 4 kali, maka x = 0, 1, 2, 3, 4. Namun jika percobaan dilakukan sebanyak n kali, maka x = 0, 1, 2, …, n.
Jika nilai peluang x kita hitung, maka akan diperoleh distribusi peluang X yang disebut sebagai distribusi binomial.
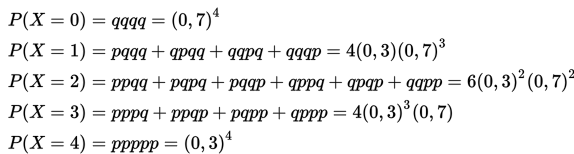
Dengan demikian, dapat disimpulkan bahwa jika percobaan binomial mempunyai peluang keberhasilan p dan peluang kegagalan q = 1 – p , maka distribusi peluang untuk variabel acak binomial x sama dengan banyaknya keberhasilan dalam n percobaan yang bebas, yaitu :
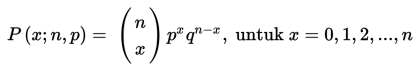
S1
Keseluruhan subjek dalam penelitian disebut ….
S2
Sebuah perusahaan otomotif hendak melakukan survey mengenai jenis mobil yang paling digemari warga Jakarta. Perusahaan tersebut kemudian memilih 100 orang pengendara mobil di Jakarta secara acak dan melakukan wawancara mengenai kendaraan favoritnya. Sampel dari survey ini adalah ….
S3
Pernyataan yang sesuai dengan distribusi binomial adalah ….
S4
Berikut ini yang merupakan ciri dari distribusi binomial adalah ….
S5
Pada percobaan binomial, jika peluang keberhasilan adalah p, maka peluang kegagalan adalah ….
S6
Jika percobaan binomial mempunyai peluang keberhasilan p dan kegagalan q, maka distribusi peluang untuk variabel acak binomial X (banyaknya keberhasilan dalam n percobaan yang bebas) adalah ….
S7
Contoh kasus yang tidak dapat diselesaikan dengan distribusi binomial adalah …
S8
Dalam sebuah keluarga yang memiliki 3 anak, peluang bahwa keluarga tersebut memiliki tiga anak perempuan adalah ….
S9
Distribusi binomial dirumuskan sebagai berikut :
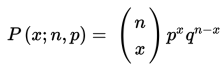
Nilai peluang kejadian binomial untuk
p = 1/3, x = 3, dan n = 4 adalah ….
p = 1/3, x = 3, dan n = 4 adalah ….
S10
Suatu variabel acak x dengan konstanta m memiliki distribusi peluang seperti pada tabel berikut :

Nilai m adalah ….

Tidak ada komentar:
Posting Komentar