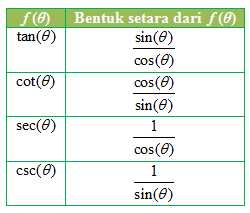
Contoh Soal Rumus Tangen Jumlah dan Selisih Dua Sudut

Contoh Soal Rumus Tangen Jumlah dan Selisih Dua Sudut - Kita telah mempelajari bahwa fungsi sinus dan kosinus merupakan dua bentuk dasar dalam trigonometri. Bentuk lain seperti tangen, kotangen, sekan, dan kosekan merupakan bentuk yang diturunkan dari kedua bentuk dasar tadi. Tabel di bawah ini menjelaskan hubungan kedua bentuk dasar tersebut dengan bentuk-bentuk trigonometri lainnya.

Hubungan Sinus dan Kosinus dengan Bentuk Trigonometri Lainnya

Pada dua topik sebelumnya, kamu telah mempelajari tentang rumus sinus dan kosinus jumlah dan selisih sudut beserta pembuktiannya. Rumus-rumus tersebut adalah:

\sin (α \pm β) = \sin α \cos β \pm \cos α \sin β

\cos (α \pm β) = \cos α \cos β \mp \sin α \sin β

Oleh karena tangen (serta bentuk lainya) diturunkan dari fungsi sinus dan kosinus, maka rumus sinus dan kosinus yang telah dipelajari sebelumnya dapat dimanfaatkan untuk menentukan rumus jumlah dan selisih untuk bentuk trigonometri lainnya.

Rumus Tangen Jumlah Dua Sudut

Langkah-langkah untuk memperoleh rumus tangen jumlah dua sudut (tan (α + β)), adalah sebagai berikut.

Ubah bentuk tan (α + β) menjadi perbandingan dari sinus dan kosinus.

\tan (α + β) = \frac{\sin (α + β)}{\cos (α + β)}

Uraikan persamaan yang terbentuk dengan menggunakan sinus dan kosinus jumlah sudut, sehingga diperoleh:

\tan (α + β) = \frac{\sin (α + β)}{\cos (α + β)} = \frac{\sin α \cos β + \cos α \sin β}{\cos α \cos β - \sin α \sin β}

Sederhanakan persamaan rasional ini dengan mengalikan tiap suku pada pembilang dan penyebut dengan $\frac{1}{\cos α \cos β}$ .

\tan (α + β) = \frac{\sin α \cos β \frac{1}{\cos α \cos β} + \cos α \sin β \frac{1}{\cos α \cos β}}{\cos α \cos β \frac{1}{\cos α \cos β} - \sin α \sin β \frac{1}{\cos α \cos β}}

\Leftrightarrow \tan (α + β) = \frac{\sin α \cos β \frac{1}{\cos α \cos β} + \cos α \sin β \frac{1}{\cos α \cos β}}{\cos α \cos β \frac{1}{\cos α \cos β} - \sin α \sin β \frac{1}{\cos α \cos β}}

\Leftrightarrow \tan (α + β) = \frac{\frac{\sin α}{\cos α} + \frac{\sin β}{\cos β}}{1 - \frac{\sin α \sin β}{\cos α \cos β}}

Sederhanakan persamaan terakhir dengan mensubstitusikan $\tan α = \frac{\sin α}{\cos α}$ dan $\tan β = \frac{\sin β}{\cos β}$ , sehingga diperoleh rumus tangen jumlah dua sudut yaitu:

\tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \tan β}

Rumus Tangen Selisih Dua Sudut

Langkah yang sama dengan menentukan rumus tangen jumlah dua sudut (tan (α + β)) dapat digunakan untuk memperoleh rumus tangen selisih dua sudut (tan (α - β)). Kamu juga dapat menerapkan langkah yang serupa untuk menentukan rumus jumlah dan selisih dua sudut pada bentuk trigonometri lainnya (kotangen, sekan dan kosekan). Adapun rumus tangen jumlah dua sudut (tan (α + β)) diperoleh melalui penguraian sebagai berikut.

\tan (α - β) = \frac{\sin (α - β)}{\cos (α - β)}

\Leftrightarrow \tan (α - β) = \frac{\sin α \cos β - \cos α \sin β}{\cos α \cos β + \sin α \sin β}

\Leftrightarrow \tan (α - β) = \frac{\sin α \cos β \frac{1}{\cos α \cos β} - \cos α \sin β \frac{1}{\cos α \cos β}}{\cos α \cos β \frac{1}{\cos α \cos β} + \sin α \sin β \frac{1}{\cos α \cos β}}

\Leftrightarrow \tan (α - β) = \frac{\sin α \cos β \frac{1}{\cos α \cos β} - \cos α \sin β \frac{1}{\cos α \cos β}}{\cos α \cos β \frac{1}{\cos α \cos β} + \sin α \sin β \frac{1}{\cos α \cos β}}

\Leftrightarrow \tan (α - β) = \frac{\frac{\sin α}{\cos α} - \frac{\sin β}{\cos β}}{1 + \frac{\sin α \sin β}{\cos α \cos β}}

Sederhanakan persamaan terakhir dengan mensubstitusikan

\tan α = \frac{\sin α}{\cos α} d a n \tan β = \frac{\sin β}{\cos β}

, sehingga diperoleh rumus tangen jumlah dua sudut yaitu:

$\tan (α - β) = \frac{\tan α - \tan β}{1 + \tan α \tan β}$

Selain dengan cara di atas, rumus tangen selisih dua sudut (tan (α - β)) juga dapat diperoleh dengan memanfaatkan rumus tangen jumlah dua sudut (tan (α + β)). Caranya adalah dengan mengganti β dengan -β pada rumus tangen jumlah dua sudut. Detail pembuktiannya dapat kamu kerjakan sendiri sebagai latihan.

Dengan demikan, rumus tangen jumlah dan selisih dua sudut adalah:

$\tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \tan β}$

$\tan (α - β) = \frac{\tan α - \tan β}{1 + \tan α \tan β}$

Contoh Soal Rumus Tangen Jumlah dan Selisih Dua Sudut

$\tan (α - β) = \frac{\tan α - \tan β}{1 + \tan α \tan β}$

SOAL 1

$\tan (α - β) = \frac{\tan α - \tan β}{1 + \tan α \tan β}$

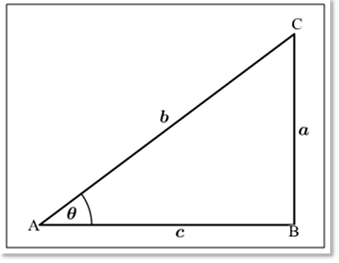
Pada segitiga siku-siku ABC berikut ini. Nilai dari tan θ adalah ….

SOAL 2

tan θ juga dapat didefinisikan sebagai ….

SOAL 3

Nilai dari

\frac{\tan 85^{\circ} - \tan 40^{\circ}}{1 + \tan 85^{\circ} \tan 40^{\circ}}

adalah ….

SOAL 4

Bentuk yang setara dengan tan (x + x) adalah ….

SOAL 5

Nilai dari tan 105⁰ adalah …

SOAL 6

Nilai dari tan 15⁰ adalah ….

SOAL 7

Diketahui α dan β merupakan sudut lancip. Jika α = 45⁰ dan

\cos β = \frac{3}{5}

, maka nilai dari tan (α + β) adalah ….

SOAL 8

Diketahui x dan y merupakan sudut lancip. Jika

\sin x = \frac{4}{5}

dan

\cos y = \frac{12}{13}

, maka nilai tan (x - y) adalah ….

SOAL 9

Pada suatu nilai (a, b) tertentu, nilai dari bentuk

\frac{\tan a + \tan b}{1 - \tan a \tan b}

membesar tanpa batas. Pernyataan berikut ini yang benar tentang nilai a dan b adalah ….

SOAL 10

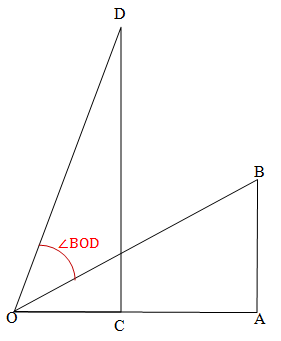
Perhatikan gambar berikut ini.

Jika panjang AB, CD, OC, dan OA berturut-turut adalah 7, 12, 5 dan 17 satuan, maka besar ∠BOD adalah ….

Tentang: MIA kelas 11

Contoh Soal Rumus Tangen Jumlah dan Selisih Dua Sudut

Rumus Tangen Jumlah Dua Sudut

Rumus Tangen Selisih Dua Sudut

Share:

Artikel Terkait

Tidak ada komentar:

Posting Komentar