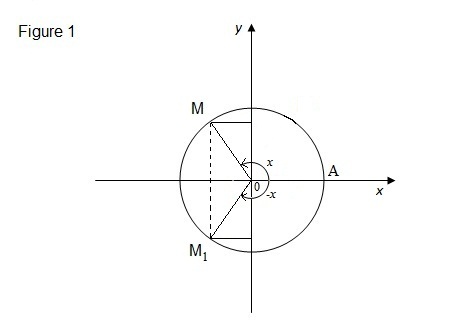
Kesimetrian Fungsi Trigonometri - Untuk menyelidiki simetri fungsi trigonometri mari kita menyadari sudut sembarang AOM, sama dengan x dan sudut invers AOM1, pada unit lingkaran (lihat gambar 1). Kita asumsikan bahwa M mempunyai koordinat a dan b, jadi M1 mempunyai koordinat adan –b.
Dengan demikian, sin x=b dan sin(-x)=-b. Bandingkan persamaan terakhir yang kita simpulkan(-x)=-sin x (karakteristik sinus yang ganjil). Berargumen secara analog, kita mendapat cos x=a and cos (-x)=a. Karenanya cos(-x)=cos x (karakteristik cosinus genap).
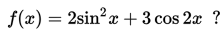
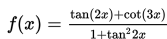
Tentang:
Matematika
Dengan demikian, sin x=b dan sin(-x)=-b. Bandingkan persamaan terakhir yang kita simpulkan(-x)=-sin x (karakteristik sinus yang ganjil). Berargumen secara analog, kita mendapat cos x=a and cos (-x)=a. Karenanya cos(-x)=cos x (karakteristik cosinus genap).

Contoh 1.
Apakah fungsi berikut ganjil atau genap:
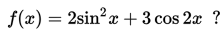
Solusi
Mari kita cari f(-x)
terlebih dahulu:
Transformasi f(-x) dikarenakan simetri sinus dan cosinus: terlebih dahulu:
Karena kita mendapat f(x)=f(-x) maka ini mengimplikasikan bahwa f(x) adalah genap.
Adalah mudah untuk memeriksa karakteristik ganjil tangen dan cotangen. Nyatanya,
Contoh 2.
Apakah fungsi berikut ganjil atau genap:
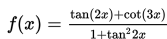
Solusi
Seperti contoh 1, pertama kita mencari f(-x):
Transformi f(-x) dikarenakan simetri tangen dan cotangen Karena kita mendapat f(-x)=-f(x) ini mengimplikasikan bahwa f(x) adalah ganjil.

Tidak ada komentar:
Posting Komentar