Membatasi Domain untuk Menghasilkan Invers - Pada pelajaran ini kita akan belajar tentang bagaimana cara membatasi domain suatu fungsi yang tidak invertible dan mengubahnya menjadi suatu fungsi yang invertible (mempunyai invers)
Tentang:
Matematika
 |
| Membatasi Domain untuk Menghasilkan Invers |
Ingat kembali bahwa agar suatu fungsi invertible, maka fungsi tersebut haruslah merupakan dimana untuk setiap nilai x, terdapat tepat satu nilai y.
Contoh 1: Perhatikan fungsi yang dideskripsikan oleh tabel di bawah ini
x y
1 2
2 3
3 2
4 -1
Fungsi ini bukan satu-satu karena keduanya baik 1 dan 3 dikirim ke 2. Karenanya ini bukan fungsi invertible.
Satu cara untuk memeriksa apakah fungsi ini invertible adalah dengan menggunakan tes garis horisontal. Karenanya, untuk setiap garis horisontal seharusnya hanya melintasi grafik fungsi sekali. Pada contoh di atas jika kita menggambar garis horisontal pada y=2 maka ini akan melintasi grafik dua kali (pada x=1 dan x=3) dan karenanya gagal pada tes garis horisontal.
Sekarang kita dapat membatasi domain fungsi bukan invertible menjadi fungsi invertible.
Contoh 2: Batasi domain fungsi y=x2 untuk membuatnya invertible.
Adalah sangat jelas bahwa ini bukan fungsi invertible karena garis horisontal pada y=1 melintasi grafik dua kali (pada x=-1 dan x=1). Kenyataannya untuk setiap nilai y yang positif garis horisontal melintasi grafik dua kali. Karenanya kita mempunyai dua pilihan untuk membatasi domain fungsi untuk membuatnya invertible.
Pilihan 1: Batasi domain untuk membuat nilai x lebih besar dari atau sama dengan 0.
Pilihan 2: Batasi domain pada nilai x lebih kecil atau sama dengan 0.
Kedua pilihan tersebut akan menghasilkan fungsi satu-satu dan invers.
Sebagai catatan akhir, jika kita menggambar sebuah fungsi dan inversnya maka keduanya merupakan hasil pencerminan satu sama lain terhadap garis y=x. Dengan kata lain, jika meletakkan sebuah cermin di sepanjang garis y=x, maka kita akan melihat bahwa invers fungsi berada di dalam cermin.
Contoh 3: Berikut ini adalah grafik y=x3 dan inversnya y=x1/3
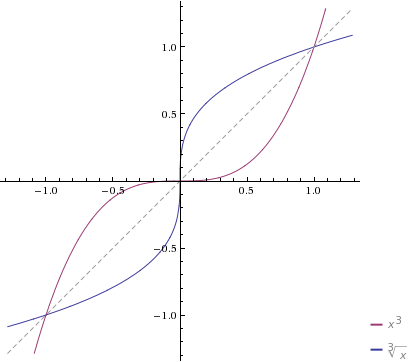
Garis titik-titik adalah y=x dan kita dapat melihat bayangan cermin di sini.
Tidak ada komentar:
Posting Komentar