Hukum Gravitasi Universal newton
Newton mempostulatkan bahwa tiap benda mengadakan gaya tarik pada benda lain yang sebanding dengan massa kedua benda dan berbanding terbalik dengan kuadrat jarak pisah antara kedua benda tersebut.
Secara matematis dapat dituliskan sebagai berikut:
Kemudian agar ruas kanan dan kiri menjadi setara maka ruas kanan perlu dikalikan suatu konstanta yang disebut dengan konstanta gravitasi universal.
Sehingga persamaan diatas menjadi:
dengan:
F = gaya tarik kedua benda
m = massa benda
r = jarak kedua benda
G = konstanta gravitasi universal (Nm2/kg2)
Dari persamaan diatas terlihat bahwa semakin besar jarak kedua benda maka akan menghasilkan gaya tarik yang lebih kecil.
Gaya gravitasi yang bekerja antara dua benda merupakan gaya aksi-reaksi. Benda 1 menarik benda 2 dan sebagai reaksinya benda 2 menarik benda 1. Menurut hukum III Newton, kedua gaya tarik ini sama besar tetapi berlawanan arah (Faksi = – Freaksi).
Jika suatu benda dipengaruhi oleh dua buah gaya gravitasi atau lebih, maka resultan gaya gravitasi yang bekerja pada benda tersebut dihitung berdasarkan penjumlahan vektor.
Bagaimana cara menentukan nilai konstanta gravitasi universal G?
Cara menentukkan nilai konstanta gravitasi universal G adalah dengan mengukur gaya gravitasi dua buah benda yang sudah diketahui massa dan jarak benda tersebut.
Para ilmuan menentukkan nilai konstanta gravitasi universal berdasarkan data yang didapat dari percobaan Sir Henry Cavendish. Cavendish melakukan percobaan untuk menghitung massa jenis bumi dengan menggunakan alat torsion balance dalam bahasa indonesia lebih sering dikenal sebagai neraca cavendish.
Gambar berikut adalah versi modern dari torsion balance
 |
Prinsip dari neraca cavendish:
1. Gaya gravitasi yang timbul menarik benda dengan massa kecil ke benda yang massanya lebih besar, m1 bergerak ke m2. Pergerakan m1 menyebabkan lengan yang tegak ikut berputar.
2. posisi akhir m1 atau m1 berhenti bergerak ketika gaya oleh kwarsa sama dengan gaya gravitasi dua benda.
3. pembelokan sinar menunjukan bahwa kwarsa telah berputar
Setelah dihitung didapat nilai G adalah 6.674281672 10-11 Nm2/kg2
Kuat Medan Gravitasi
Besarnya kuat medan gravitasi ditunjukkan dengan besarnya percepatan gravitasi. Semakin besar percepatan gravitasi maka akan menghasilkan kuat medan gravitasinya yang semakin besar. Besarnya percepatan gravitasi akibat gaya gravitasi dapat dihitung dengan hukum II Newton dan hukum gravitasi Newton.
Percepatan a adalah percepatan akibat gravitasi bumi dan diberi simbol g.
Keterangan:
g : percepatan gravitasi (m/s2 atau N/kg)
G : tetapan umum gravitasi (Nm2/kg2)
M : massa bumi (kg)
r : jari-jari bumi (m)
Untuk benda yang terletak dekat permukaan bumi maka r µR (jari-jari benda dapat dianggap sama dengan jari-jari bumi), maka persamaannya menjadi menjadi:
Tetapan g0 disebut percepatan akibat gravitasi bumi di permukaan bumi. Percepatan akibat gravitasi tidak bergantung pada bentuk, ukuran, sifat, dan massa benda yang ditarik, tetapi percepatan ini dipengaruhi oleh ketinggian kedalaman dan letak lintang. Seperti yang kita ketahui bahwa jari-jari bumi tidak rata. Jari-jari bumi di dekat kutub lebih kecil dari pada di katulistiwa. Hal ini menyebabkan percepatan gravitasi bumi ke arah kutub makin besar. Percepatan gravitasi bumi terkecil berada di ekuator.
Percepatan akibat gravitasi bumi pada ketinggian h dari permukaan bumi dapat dihitung melalui persamaan berikut..
Seperti halnya dengan gaya gravitasi, percepatan merupakan besaran vektor. Maka untuk menentukan percepatan gravitasi pada suatu titik yang diakibatkan oleh dua benda dapat dilakukan dengan cara menjumlahkan vektor-vektor percepatan gravitasinya.
Aplikasi Hukum Gravitasi Newton
Menghitung massa Bumi
Sebuah benda bermassa m yang berada di permukaan bumi akan mengalami percepatan gravitasi g sehingga berat benda tersebut memenuhi persamaan
Kemudian jika ada benda bermassa m berada di permukaaan bumi yang jaraknya dari pusat bumi adalah r, sedangkan massa bumi M, maka akan berlaku persamaan
disubtitusikan kedua persamaan diatas, sehingga diperoleh
Kita masukan nilai jari-jari bumi yaitu 6.38 x 106 m, g = 9.8 m/s2, sehingga massa bumi kurang lebih 6 x 1024 kg
Menghitung massa matahari
Massa matahari dapat dihitung dengan menggunakan persaamaan-persamaan gerak bumi mengelilingi matahari. Bumi tetap pada orbitnya karena keseimbangan dua gaya yang bekerja pada bumi, yaitu gaya tarik matahari F dan gaya sentripetal Fsp
Besar gaya tarik matahari terhadap bumi dapat dirumuskan sebagai berikut
Karena diasumsikan lintasan gerak bumi berua lingkaran, maka berlaku persamaan gerak melingkar yaitu:
Disubtitusikan kedua persamaan diatas,
Kecepatan adalah Jarak tempuh dibagi waktu tempuh. Bumi menempuh lintasan satu putaran penuh dalam waktu T, sehingga
Diketahui bahwa jari-jari rata-rata orbit bumi rB = 1,5 × 1011 m dan periode bumi dalam mengelilingi matahari TB = 1 tahun = 3 × 107 s.
Masukan nilai diatas maka kita dapat menemukan massa matahari
Menghitung kecepatan Satelit
kecepatan satelit mengelilingi bumi dapat dihitung dengan memanfaatkan hukum gravitasi.
Pertama kita misalkan massa bumi M dan jari-jari bumi R, jika ada satellit yang mempunyai massa m bergerak mengelilingi bumi pada ketinggian h dari permukaan bumi, maka berlaku persamaan-persamaan berikut:
Jarak satelit dari pusat bumi sama dengan jari-jari bumi ditambah dengan ketinggian satelit dari permukaan bumi (r = R + h), maka
Menghitung jarak Orbit satelit bumi
Kelajuan satelit bumi dapat dihitung dengan menyamakan gaya gravitasi satelit dan gaya sentripetalnya.
apabila periode orbit satelit sama dengan periode rotasi bumi (orbit geosinkron), maka jari-jari orbit satelit dapat ditentukan sebagai berikut:
Kecepatan Lepas
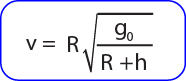
Kecepatan lepas adalah kecepatan minimum suatu benda agar saat benda tersebut dilemparkan ke atas tidak dapat kembali lagi. Kecepatan lepas sangat dibutuhkan untuk menempatkan satelit buatan pada orbitnya atau pesawat ruang angkasa. Kecepatan lepas (vl) tidak bergantung pada massa benda. Akan tetapi untuk mempercepat benda sampai mencapai kecepatan lepas diperlukan energi yang sangat besar dan tentunya bergantung pada massa benda yang ditembakkan. Besarnya kecepatan lepas yang diperlukan oleh suatu benda sangat erat kaitannya dengan energi potensial gravitasi yang dialami oleh benda tersebut. Besar kecepatan lepas dirumuskan sebagai berikut:























Tidak ada komentar:
Posting Komentar