Gerak Harmonik Sederhana
Kita tidak sering mendengar istilah gerak harmonik sederhana dalam kehidupan sehari-hari. Tetapi tanpa sadar kita telah mengamati gerak harmonik sederhana dalam keseharian kita. Contoh gerak harmonik sederhana dapat kita lihat pada ayunan bandul sederhana atau getaran pada pegas.
Agar lebih mudah memahami tentang gerak harmonik sederhana, perhatikan gambar benda yang diikat dengan pegas dibawah ini:
Misalkan massa benda adalah m dan lantai dianggap licin sehingga tidak ada gaya gesek antara benda dan lantai. Mula-mula pegas tidak ditekan ataupun ditarik, benda dalam keadaan diam pada posisi x = 0. Posisi tersebut disebut posisi kesetimbangan.
Berdasarkan hukum Hook jika benda digeser ke posisi x, pegas akan mengerjakan gaya pada benda yang besarnya sebanding dengan posisinya. Secara matematis dapat dituliskan sebagai berikut:
Dengan Fs adalah gaya pemulih (restoring force). Disebut gaya pemulih karena gaya tersebut selalu mengarah ke posisi kesetimbangan. Jadi yang dimaksud gaya pemulih adalah Gaya yang dilakukan pegas untuk mengembalikan benda pada posisi keseimbangan.
Tanda negatif menunjukkan bahwa gaya pemulih selalu memiliki arah yang berlawanan dengan simpangannya. Ketika benda ditarik sehingga benda berada disebelah kanan posisi kesetimbangan ( x = +), gaya pemulih mengarah ke kiri.
Begitu pula sebaliknya, ketika benda ditekan sehingga benda berada disebelah kiri(x = -) dari posisi kesetimbangan maka gaya pemulih mengarah ke kanan.
Jika benda ditarik dari posisi kesetimbangan kemudian dilepas, benda akan mengalami percepatan sebagai konsekuensi adanya gaya yang bekerja. Dengan adanya gaya yang bekerja, benda tersebut dapat kita modelkan sebagai partikel yang mengalami gaya, sehingga apabila kita aplikasikan hukum II Newton dan hukum Hook diatas dapat diperoleh:
Berdasarkan persamaan diatas terlihat bahwa percepatan benda sebanding dengan posisinya dan arah percepatan benda berlawanan dengan perpindahan benda dari posisi kesetimbangan. Sistem seperti itulah yang dimaksud dengan gerak harmonik sederhana.
Jadi benda dikatakann bergerak Harmonik sederhana jika percepatan benda berbanding lurus dengan posisinya dan arah percepatan benda tersebut berlawanan dengan arah perpindahan dari posisi kesetimbangan.
Periode dan frekuensi Gerak harmonik sederhana
Periode dan frekuensi pada pegas
Periode dan frekuensi sistem beban pegas hanya bergantung pada massa dan konstanta gaya pegas. Secara matematis periode pegas dapat dituliskan:
Frekuensi pegas berbanding terbalik dengan periode pegas sehingga besar frekuensi pegas dapat dinyatakan sebagai berikut:
dengan:
T = Periode (s)
f = frekuensi getaran pegas(Hz)
m = massa beban (kg)
k = tetapan pegas (N/m)
Periode dan Frekuensi Bandul Sederhana
Sebuah bandul sederhana terdiri atas sebuah beban bermassa m yang digantung di ujung tali yang panjangnya l, massa tali diabaikan. Jika beban ditarik ke satu sisi dan dilepaskan, maka beban berayun melalui titik keseimbangan menuju ke sisi yang lain.
Perhatikan Ilustrasi bandul sederhana berikut:
 |
Jika sudut q kecil maka bandul melakukan getaran harmonik. Periode dan frekuensi getaran pada bandul sederhana sama seperti pada pegas. Artinya, periode dan frekuensinya dapat dihitung dengan menyamakan gaya pemulih dan gaya sentripetal. Periode dan frekuensi bandul sederhana tidak bergantung pada massa dan simpangan bandul, tetapi hanya bergantung pada panjang tali dan percepatan gravitasi setempat.
Periode bandul sederhana dirumuskan sebagai berikut:
Frekuensi bandul berbanding terbalik dengan periode pegas sehingga besar frekuensi pegas dapat dinyatakan sebagai berikut:
dengan:
T = Periode (s)
f = frekuensi bandul (Hz)
l = panjang tali (m)
g = percepatan gravitasi (m/s2)
Persamaan Gerak Harmonik Sederhana
Persamaan getaran harmonik diperoleh dengan memproyeksikan gerak melingkar terhadap sumbu untuk titik yang bergerak beraturan. Akan tetapi saya tidak akan menuliskannya disini. Kali ini saya hanya kan menuliskan hasilnya saja tidak menjelaskan bagaimana asal dari rumus tersebut.
Simpangan gerak harmonik sederhana
Simpangan gerak harmonik sederhana dapat dirumuskan sebagai berikut
Besar sudut dalam fungsi sinus (q ) disebut sudut fase.
Jika partikel mula-mula berada pada posisi sudut q0, maka persamaanya dapat dituliskan sebagai berikut.
dengan:
Y = simpangan (m)
f = frekuensi (Hz)
t = waktu (s)
q0 = sudut awal (rad)
w = frekuensi sudut (rad/s)
A = ampitudo (m)
T = periode (s)
Sudut fase getaran harmoniknya adalah sebagai berikut.
F disebut fase getaran, fase getaran harmonik dapat dituliskan sebagai berikut:
Apabila sebuah benda bergetar harmonik mulai dari t = t1 hingga t = t2, maka beda fase benda tersebut adalah sebagai berikut:
Beda fase dalam getaran harmonik dinyatakan dengan nilai mulai dari nol sampai dengan satu. Bilangan bulat dalam beda fase dapat dihilangkan, misalnya beda fase 2¼ cukup ditulis sebagai beda fase ¼.
Kecepatan Gerak Harmonik Sederhana
Kecepatan benda yang bergerak harmonik sederhana dapat diperoleh dari turunan pertama persamaan simpangan.
atau
Mengingat nilai maksimum dari fungsi cosinus adalah satu, maka kecepatan maksimum (vmaks) gerak harmonik sederhana adalah sebagai berikut.
dengan:
vy = kecepatan terhadap sumbu y (m/s)
vmaks = kecepatan maksimum(m/s)
Percepatan Gerak Harmonik Sederhana
Percepatan benda yang bergerak harmonik sederhana dapat diperoleh dari turunan pertama persamaan kecepatan atau turunan kedua persamaan simpangan.
Karena nilai maksimum dari simpangan adalah sama dengan amplitudonya (y = A), maka percepatan maksimumnya (amaks) gerak harmonik sederhana adalah sebagai berikut.
Energi Pada Gerak Harmonik Sederhana
Benda yang bergerak harmonik memiliki energi potensial dan energi kinetik. Jumlah kedua energi ini disebut energi mekanik.
Energi Kinetik Gerak Harmonik
Energi kinetik pada gerak harmonik sederhana dapat ditulis sebagai berikut:
Energi kinetik juga dapat dituliskan dalam bentuk lain yang lebih sederhana seperti berikut
Energi kinetik maksimum pada gerak harmonik dicapai ketika berada di titik setimbang. Sedangkan energi kinetik minimum dicapai ketika berada di titik balik.
Energi Potensial Gerak Harmonik Sederhana
Besar gaya yang bekerja pada getaran harmonik selalu berubah yaitu berbanding lurus dengan simpangannya (F = ky). Secara matematis energi potensial yang dimiliki gerak harmonik dirumuskan sebagai berikut.
Energi Mekanik
Energi mekanik sebuah benda yang bergerak harmonik adalah jumlah energi kinetik dan energi potensialnya.
Berdasarkan persamaan diatas energi mekanik suatu benda yang bergetar harmonik tidak tergantung waktu dan tempat. Jadi, energi mekanik sebuah benda yang bergetar harmonik dimanapun besarnya sama.
Agar lebih mudah memahami hubungan nilai Ep dan Ek, coba perhatikan grafik dan ilustrasi Hubungan Ek dan Ep dibawah ini:
 |
| *physics for scientists and engineers |
Kecepatan Benda yang Bergera Harmonik Sederhana
Kecepatan maksimum benda atau pegas yang bergetar harmonik dapat dihitung dengan menyamakan persamaan kinetik dan energi total mekaniknya.
Sedangkan untuk menghitung kecepatan benda di titik sembarang dilakukan dengan menggunakan persamaan kekekalan energi mekanik
dengan:
vmaks = kecepatan maksimum (m/s)
A = amplitudo (m)
k = konstanta pegas (N/m)
m = massa benda (kg)





















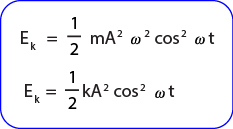







Tidak ada komentar:
Posting Komentar