Contoh Soal Aplikasi Deret Geometri Tak Hingga Pada Pemecahan Masalah - Berbagai masalah yang sering dijumpai di sekeliling kita ternyata dapat dipecahkan dengan bantuan deret geometri tak hingga. Jika kita amati sebuah bola yang jatuh dari ketinggian tertentu dan menyentuh lantai, bola akan memantul kemudian jatuh dan memantul lagi, dan seterusnya. Gerakan bola tersebut membentuk suatu lintasan yang panjangnya dapat dihitung dengan menerapkan konsep deret geometri tak hingga. Deret ini juga dapat menjadi solusi untuk membuktikan nilai dari bilangan desimal berulang. Dalam geometri, deret tersebut digunakan untuk menghitung jumlah seluruh luas dan keliling bangun datar yang di dalamnya dibuat lagi tak terhingga banyaknya bangun datar yang sebangun. Mari perkaya wawasanmu tentang penerapan deret geometri tak hingga dengan mempelajari topik ini.
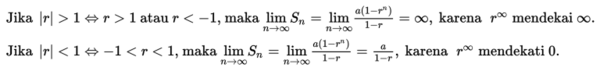
dengan:
S∞ = jumlah semua suku deret geometri tak hingga
a = U1 = suku pertama
r = = rasio (pembanding)
Tentang:
Matematika Ipa kelas 12
Jika suatu deret geometri, Sn = U1 + U2 + U3 + ... + Un - 1 + Un dengan n mendekati tak hingga, maka deret geometri tersebut dikatakan sebagai deret geometri tak hingga dan ditulis dengan:
S∞ = U1 + U2 + U3 + ... + Un - 1 + ....
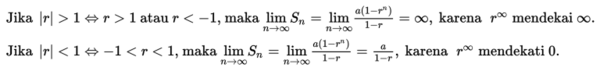
Dengan demikian, rumus jumlah deret geometri tak hingga untuk |r| < 1, r ≠ 0 adalah:
dengan:
S∞ = jumlah semua suku deret geometri tak hingga
a = U1 = suku pertama
r = = rasio (pembanding)
SOAL 1
Sebuah bola dijatuhkan dari ketinggian 15 m. Setiap kali sesudah jatuh mengenai lantai, bola itu dipantulkan lagi dan mencapai seperempat tinggi sebelumnya. Panjang seluruh lintasan yang dilalui bola itu sampai berhenti adalah ...
SOAL 2
Sebuah bola jatuh dari ketinggian 6 meter dan memantul kembali dengan ketinggian kali tinggi sebelumnya. Keadaan ini berlangsung terus-menerus hingga bola berhenti. Panjang lintasan bola jatuh adalah ….
SOAL 3
Diketahui sebuah segitiga siku-siku sama kaki dengan panjang sisi siku-sikunya 8 cm. Dalam segitiga tersebut terdapat segitiga siku-siku sama kaki yang merupakan hasil proyeksi segitiga siku-siku sama kaki pertama, dan begitu seterusnya. Panjang semua sisi miring yang terbentuk adalah ….
SOAL 4
Diketahui sebuah segitiga siku-siku sama kaki dengan panjang sisi siku-sikunya 12 cm. Dalam segitiga tersebut terdapat segitiga siku-siku sama kaki yang merupakan hasil dari proyeksi segitiga siku-siku sama kaki yang pertama, dan seterusnya. Panjang semua sisi penyiku yang terbentuk adalah ….
SOAL 5
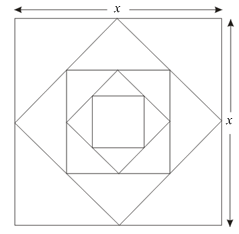
Persegi seperti gambar di bawah ini jika diteruskan jumlah luasnya adalah ….

SOAL 6
Sebuah bola pingpong dijatuhkan ke lantai dari ketinggian 2 meter. Setiap kali memantul, bola tersebut mencapai ketinggian tiga per empat dari ketinggian sebelumnya. Panjang lintasan bola tersebut dari pantulan ke-3 sampai berhenti adalah ….
SOAL 7
Diketahui jumlah suatu deret geometri tak hingga adalah 36, sedangkan jumlah semua suku bernomor ganjil adalah 27. Rasio deret tersebut adalah ....
SOAL 8
Di dalam ∆ABC, dbuat segitiga sama sisi lain dengan titik sudutnya berimpit dengan pertengahan sisi-sisi segitiga pertama. Selanjutnya, dibuat segitiga sama sisi dengan titik sudut yang terletak pada pertengahan sisi-sisi segitiga sebelumnya. Proses ini dilanjutkan terus menerus. Jika luas semua segitiga yang terbentuk adalah satuan luas, maka luas segitiga yang ke-6 adalah … satuan luas.
SOAL 9
Diketahui lingkaran L1 berjari-jari 5 cm adalah lingkaran luar persegi B1. Lingkaran L2menyinggung sisi-sisi bagian dalam B1 dan merupakan lingkaran luar persegi B2, demikian seterusnya. Luas semua persegi tersebut adalah ….
SOAL 10
Diketahui ∆ABC siku-siku di A. Titik B1 terletak pada BC sehingga AB1 ⏊ BC dan terbentuk ∆B1AC. Titik A1 terletak pada AC sehingga B1A1 ⏊ AC dan terbentuk ∆A1B1C. Titik B2 terletak pada BC sehingga A1B2 ⏊ BC dan terbentuk ∆B2A1C. Proses ini berlajut terus menerus. Jika panjang AB = 6 cm dan BC = 10 cm, maka jumlah luas segitiga yang terbentuk adalah … cm2.

Tidak ada komentar:
Posting Komentar