Translasi Menggunakan Matriks - Sebelum kita mempelajari tentang Translasi, ada baiknya kita mengetahui apakah yang dimaksud dengan translasi. Translasi atau geseran adalah transformasi atau perubahan setiap titik dengan jarak dan arah yang tetap.
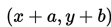
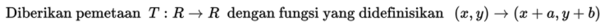
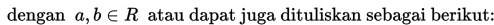
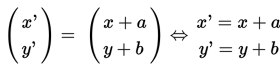
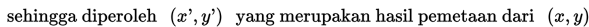
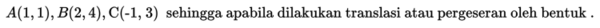
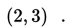
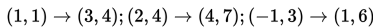
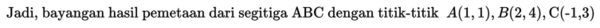
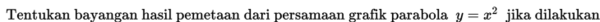
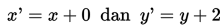
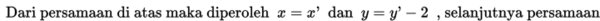
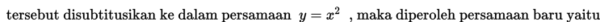
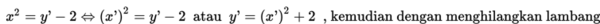
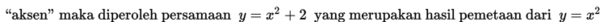
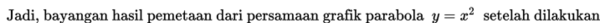
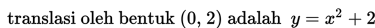

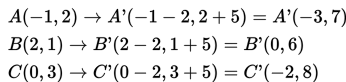


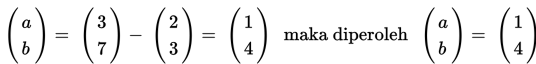
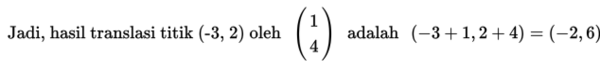
Tag :
matriks transformasi,
Tentang:
MIA kelas 12
Dalam vektor, translasi atau pergeseran adalah penambahan setiap titik (x,y) dengan vektor tertentu, misal vektor (a,b) sehingga dapat menghasilkan bayangan titik
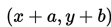
Kita dapat mendefinisikan transformasi translasi sebagai berikut:
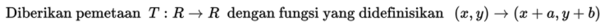
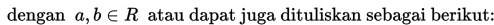
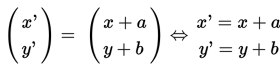
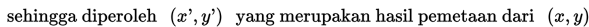
Untuk lebih jelasnya, mari kita perhatikan contoh berikut:
Contoh 1.
Tentukan bayangan hasil pemetaan dari segitiga ABC dengan titik-titik
Tentukan bayangan hasil pemetaan dari segitiga ABC dengan titik-titik
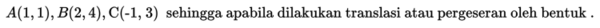
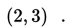
Penyelesaian:
Maka kita cukup memetakan titik-titik sudutnya sehingga diperoleh:
Maka kita cukup memetakan titik-titik sudutnya sehingga diperoleh:
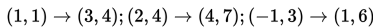
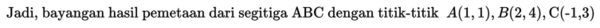
adalah A’B’C’ dengan A’(3,4), B’(4,7), dan C’(1,6).
Contoh 2.
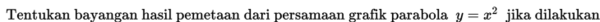
translasi atau geseran oleh bentuk (0, 2).
Penyelesaian:
Dalam kasus ini kita telah peroleh persamaannya yaitu:
Dalam kasus ini kita telah peroleh persamaannya yaitu:
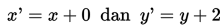
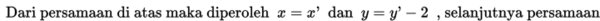
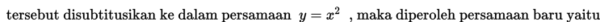
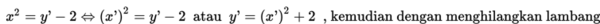
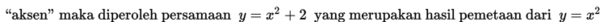
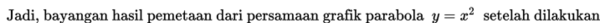
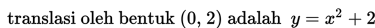
Contoh 3.

titik-titiknya yaitu A(-1, 2), B(2, 1), dan C(0,3).
Penyelesaian:
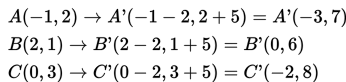
Jadi, bayangan hasil translasi dari segitiga ABC adalah A’B’C’ dengan A’(-3, 7), B’(0, 6), dan C’(-2, 8).
Contoh 4.

titik (-3, 2).
Penyelesaian:

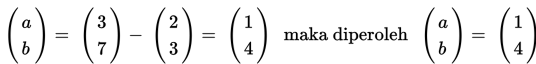
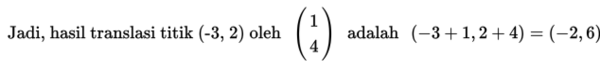
Tag :
matriks transformasi,
rumus translasi,
komposisi transformasi geometri,
contoh soal transformasi geometri refleksi,
pencerminan terhadap garis y=mx+c,
transformasi geometri kelas 12,
pencerminan terhadap garis y=2x,
contoh soal dilatasi,
Tidak ada komentar:
Posting Komentar