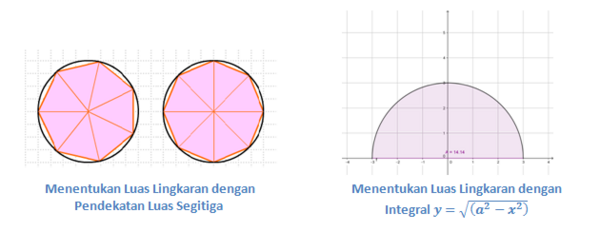
Contoh Soal Integral dengan Subsitusi Trigonometri

Contoh Soal Integral dengan Subsitusi Trigonometri - Ketika mempelajari luas lingkaran di SMP, tentu gurumu pernah menjelaskan bahwa rumus luas lingkaran dapat diperoleh dengan membagi lingkaran menjadi juring-juring yang menyerupai bentuk segitiga-segitiga kecil. Dengan demikian, luas lingkaran dapat diperoleh dengan menghampiri luas segitiga-segitiga kecil yang terbentuk. Selain dengan menggunakan pendekatan luas segitiga, luas lingkaran juga dapat diperoleh secara analitik melalui integral (integral luas).

Luas lingkaran tersebut diperoleh sebagai hasil dari pengintegralan ∫a2−x2−−−−−−√dx$\int \sqrt{a^2-x^2}dx$. Jika kita memisalkan u=a2−x2$u=a^2-x^2$, maka penyelesaiannya akan menjadi rumit. Untuk itu perlu dilakukan pensubsitusian yang dapat mempermudah peingtegralan dengan bentuk tersebut, yaitu dengan substitusi trigonometri. Integral dengan substitusi trigonometri inilah yang akan kita bahas pada topik ini. Jadi, perhatikan materi ini dengan baik ya.

Saat mempelajari konsep trigonometri, kamu tentu telah diperkenalkan dengan beberapa identitas trigonometri, yaitu:

Dengan memanfaatkan identitas tersebut, kita dapat menyelesaikan permasalahan integral luas lingkaran di atas dengan subsitusi yang melibatkan bentuk trigonometri.

Misalkan x=a.sinθ$x=a.\sin \theta$, maka dx=a.cosθdθ$dx=a.\cos \theta d\theta$, dan

a2−x2=a2−(a.sinθ)2=a2−a2.sin2θ=a2(1−sin2θ)=a2cos2θ$\begin{array}{rl}{a}^2-x^2& =a^2-(a.\sin \theta {)}^2\\ & =a^2-a^2.{\sin }^2\theta \\ & =a^2(1-{\sin }^2\theta )\\ & =a^2{\cos }^2\theta \end{array}$.

Dengan demikian diperoleh,
∫a2−x2−−−−−−√dx=∫a2cos2θ−−−−−−−√.acosθdθ=∫acosθ.acosθdθ=∫a2cos2θdθ=a2∫1+cos2θ2dθ=a2(θ2+sin2θ4)+c$\begin{array}{rl}\int \sqrt{a^2-x^2}dx& =\int \sqrt{a^2{\cos }^2\theta }.a\cos \theta d\theta \\ & =\int a\cos \theta .a\cos \theta d\theta \\ & =\int a^2{\cos }^2\theta d\theta \\ & =a^2\int \frac{1+\cos 2\theta }{2}d\theta \\ & =a^2\left(\frac{\theta }{2}+\frac{\sin 2\theta }{4}\right)+c\end{array}$

Jadi hasil pengintegralan ∫a2−x2−−−−−−√dx$\int \sqrt{a^2-x^2}dx$ dalam variabel θ$\theta$ yaitu a2(θ2+sin2θ4)+c$a^2\left(\frac{\theta }{2}+\frac{\sin 2\theta }{4}\right)+c$.

Susy Gala dirceclub https://verystream.com/stream/THQPTCMwbfh

Pada penjelasan di atas telah dibahas salah satu teknik pengintegralan dengan subsitusi trigonometri. Konsep trigonometri yang digunakan yaitu identitas trigonometri. Dengan demikian, tentu ada hubungan antara bentuk aljabar dari persoalan yang akan diintegralkan dengan identitas trigonometri, yaitu bentuk a2−x2−−−−−−√$\sqrt{a^2-x^2}$, a2+x2−−−−−−√$\sqrt{a^2+x^2}$, dan x2−a2−−−−−−√$\sqrt{x^2-a^2}$. Hubungan tersebut dijelaskan pada tabel berikut.

Berdasarkan tabel di atas, dapat kita lihat bahwa pengintegralan dari bentuk-bentuk a2−x2−−−−−−√$\sqrt{a^2-x^2}$, a2+x2−−−−−−√$\sqrt{a^2+x^2}$, dan x2−a2−−−−−−√$\sqrt{x^2-a^2}$, akan lebih mudah diselesaikan dengan menggunakan pemisalan trigonometri, yaitu:

• x=asinθ$x=a\sin \theta$ untuk bentuk a2−x2−−−−−−√$\sqrt{a^2-x^2}$;
• x=atanθ$x=a\tan \theta$ untuk bentuk a2+x2−−−−−−√$\sqrt{a^2+x^2}$; dan
• x=asecθ$x=a\sec \theta$ untuk bentuk x2−a2−−−−−−√$\sqrt{x^2-a^2}$.

SOAL 1

Hasil pengintegralan ∫1+tan2xdx$\int 1+{\tan }^{2}xdx$ adalah ....

SOAL 2

Jika x=3sinθ$x=3\sin \theta$, maka hasil dari ∫9−x2√x2dx$\int \frac{\sqrt{9-x^2}}{x^2}dx$dalam variabel θ$\theta$ adalah ….

SOAL 3

Nilai dari ∫21dxx2x2−1√${\int }_1^2\frac{dx}{x^2\sqrt{x^2-1}}$ adalah ….

SOAL 4

Diketahui ∫π0πx−1x2+π2√dx=t−∫π40secθdθ${\int }_0^{\pi }\frac{\pi x-1}{\sqrt{x^2+{\pi }^2}}dx=t-{\int }_0^{\frac{\pi }{4}}\sec \theta d\theta$. nilai t$t$ yang memenuhi persamaan tersebut adalah ….

SOAL 5

Nilai p$p$ yang memenuhi persamaan ∫−1−2x2+2x+2−−−−−−−−−√dx=p∫π40sec3θdθ${\int }_{-2}^{-1}\sqrt{x^2+2x+2}dx=p{\int }_0^{\frac{\pi }{4}}{\sec }^3\theta d\theta$adalah....

SOAL 6

Nilai dari ∫10x1−x4−−−−−√dx${\int }_0^{1}x\sqrt{1-x^4}dx$ adalah ….

SOAL 7

Jika x$x$ adalah sisi samping dari sudut θ$\theta$ dengan 0<θ<90∘$0<\theta <{90}^{\circ }$ pada sebuah segitiga siku-siku bersisi miring 4 satuan, maka nilai dari ∫π20xdx${\int }_0^{\frac{\pi }{2}}xdx$adalah ….

SOAL 8

Diketahui ∫42x+3x3−4xdx=ab∫π302cscθ+3cotθdθ${\int }_2^4\frac{x+3}{x^3-4x}dx=\frac{a}{b}{\int }_0^{\frac{\pi }{3}}2\csc \theta +3\cot \theta d\theta$. Jika FPB(a,b)=1$(a,b)=1$, maka nilai dari a+b$a+b$ adalah ….

SOAL 9

Nilai dari ∫π0sintcost1+sin2t√dt${\int }_0^{\pi }\frac{\sin t\cos t}{\sqrt{1+{\sin }^{2}t}}dt$ adalah ….

SOAL 10

Nilai dari ∫43133t+29t2+12t−5√dt${\int }_{\frac{1}{3}}^{\frac{4}{3}}\frac{3t+2}{\sqrt{9t^2+12t-5}}dt$ adalah ….

Tentang: Matematika Ipa kelas 12

Share:

Artikel Terkait