Contoh Soal Operasi Pembagian pada Suku Banyak oleh Bentuk Linear - Operasi pembagian suku banyak yang akan kalian pelajari adalah pembagian suku banyak oleh bentuk linear dan oleh bentuk kuadrat. Pada topik ini, akan dijelaskan secara detail mengenai operasi pembagian suku banyak oleh bentuk linear. Untuk pembagian suku banyak oleh bentuk kuadrat akan kalian pelajari pada topik selanjutnya.
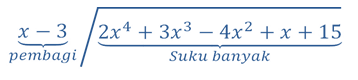
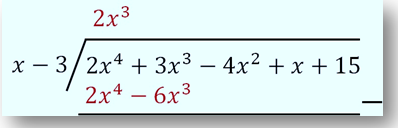
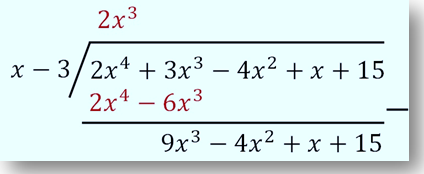
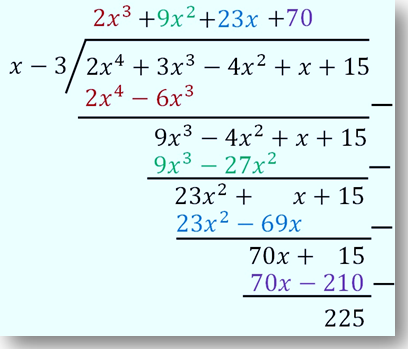
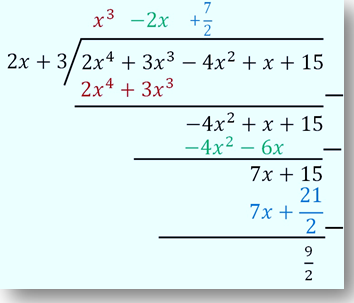
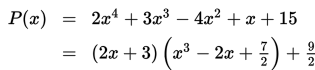
Tentang:
MIA kelas 11
Mari kita mulai dengan meninjau apa yang terjadi jika suku banyak P (x) dibagi dengan bentuk-bentuk linear bervariabel tunggal (x - k) atau (ax + b). Untuk mengetahui apa yang akan terjadi, kalian harus memahami cara pembagian suku banyak oleh bentuk linear. Ada dua cara yang bisa digunakan, yaitu metode pembagian bersusun dan metode skema.
Metode Pembagian Bersusun
Kalian tentu sudah sangat mahir melakukan pembagian suatu bilangan dengan metode bersusun bukan? Metode tersebut sudah sangat sering kalian gunakan ketika duduk di bangku SD. Tahukah kalian kalau metode tersebut dapat digunakan dalam membahas konsep pembagian suku banyak? Mari perhatikan penjelasan berikut ini.
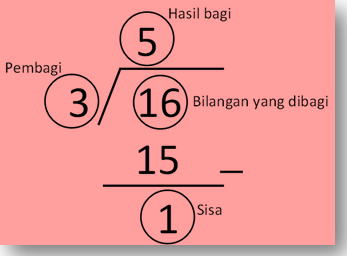
Misalkan untuk menghitung 16 : 3, dengan menggunakan metode pembagian bersusun, diperoleh:

Dapat dituliskan:
16 = (3 x 5) + 1
Bilangan yang dibagi = (Pembagi x Hasil bagi) + Sisa
Sekarang, konsep tersebut mari kita terapkan pada pembagian suku banyak.
Perhatikan contoh berikut ini.
Pembagian Bersusun oleh Bentuk Linear (x - k)
Contoh
Hasil dan sisa pembagian dari suku banyak
P (x) = 2x 4 + 3x 3 - 4x 2 + x + 15 oleh bentuk linear q (x) = x - 3
adalah ....
Penyelesaian:
Pahami langkah-langkah penyelesaian berikut ini.
Langkah 1
Menuliskan suku banyak yang dibagi P (x) dan pembaginya q (x) kedalam notasi pembagian bersusun.
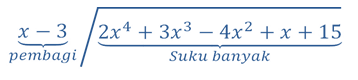
Langkah 2
Menentukan suatu suku yang apabila dikalikan dengan suku berderajat tertinggi pada pembagi q (x) akan menghasilkan suku dengan derajat tertinggi pada suku banyak yang dibagi P (x).
Pada kasus ini, 2x 3 merupakan suku yang dimaksud karena 2x 3 . x = 2x 4. Tuliskan hasil perkalian 2x 3 dengan pembagi (x - 3) dibawah suku banyak yang dibagi P (x).
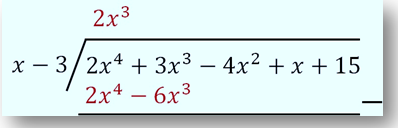
Langkah 3
Mengurangkan P (x) dengan hasil dari langkah 2.
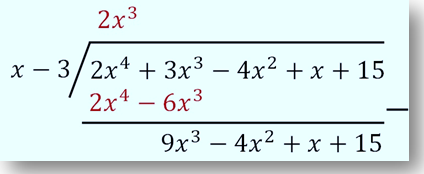
Langkah 4
Mengulang langkah 2 dan 3 hingga pembagian tidak lagi dapat dijalankan.
Pada akhir proses ini akan diperoleh pembagian bersusun sebagai berikut.
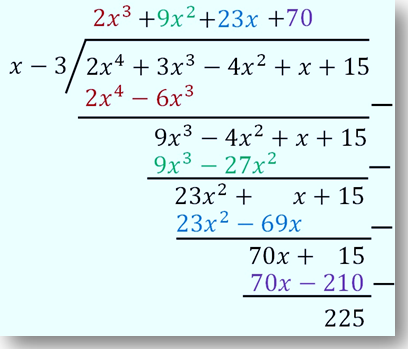
Melalui perhitungan tersebut, dapat disimpulkan:
hasil bagi = 2x 3 + 9x 2 + 23x + 70
sisa = 225
Jadi, P (x) = (x - 3) (2x 3 + 9x 2 + 23x + 70) + 225.
Pembagian Bersusun oleh Bentuk Linear (ax + b)
Contoh
Hasil dan sisa pembagian dari suku banyak
P (x) = 2x 4 + 3x 3 - 4x 2 + x + 15 oleh bentuk linear q (x) = 2x + 3
adalah ....
Penyelesaian:
Mari kita gunakan langkah yang sama seperti pada pembagian oleh bentuk (x - k), diperoleh:
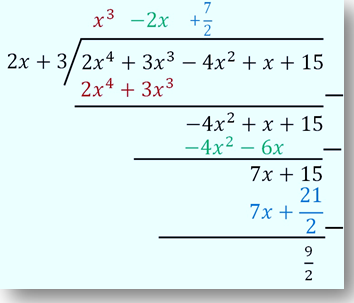
Dengan demikian,
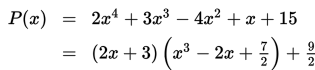
SOAL 1
Sisa pembagian suku banyak
P (x) = x 4 + 2x 3 - 42x 2 - 40x + 60
oleh q (x) = x - 6 adalah ....
SOAL 2
Hasil bagi dari pembagian suku banyak
P (x) = 2x 4 + x 3 - 5x 2 + 7x + 17
oleh q (x) = x + 2 adalah ....
SOAL 3
Sisa dari pembagian suku banyak
P (x) = 2x 5 + 3x 4 + 4x 3 + 5x 2 + 6x + 7
oleh q (x) = 2x - 1 adalah ....
SOAL 4
Hasil pembagian suku banyak
P (x) = 2x 3 + x 2 - x + 1
oleh q (x) = 2x - 5 adalah ....
SOAL 5
Bentuk yang setara dengan x 3 - 3x 2 - 7x + 5 adalah ....
SOAL 6
Hasil bagi dan sisa pembagian suku banyak
P (x) = x 4 + 2x 3 + x - 2
oleh q (x) = x + 2 adalah ..
SOAL 7
Diketahui suku banyak
P (x) = x 4 + Ax 2 + 4x + 20
mempunyai sisa 8 saat dibagi oleh q (x) = x + 2.
Nilai A yang memenuhi adalah ....
SOAL 8
Clara diminta untuk mencari hasil bagi dan sisa
pembagian suku banyak P (x) = 3x 3 + 4x 2 + 5x + 6
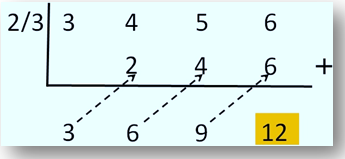
oleh q (x) = 3x - 2. Perhatikan skema yang diperoleh Clara.

Clara menyimpulkan bahwa hasil baginya adalah
3x 2 + 6x + 9 dengan sisa 12. Namun, gurunya tidak memberi poin penuh dan melingkari kesimpulan yang Clara tulis. Letak kekeliruan yang Clara buat adalah ....
3x 2 + 6x + 9 dengan sisa 12. Namun, gurunya tidak memberi poin penuh dan melingkari kesimpulan yang Clara tulis. Letak kekeliruan yang Clara buat adalah ....
SOAL 9
Dua buah suku banyak P (x) dan Q (x) selalu habis apabila dibagi dengan (x + k). Apabila R (x) adalah suku banyak hasil penjumlahan P (x) dan Q (x), maka sisa dari R (x) apabila dibagi dengan (x + k) adalah ....
SOAL 10
Suku banyak P (x) =Ax 3 + Bx 2 + Cx + D
dibagi dengan q (x) = x - 1 memberikan hasil
H (x) = 2x 2 + 3x + 1 dan sisa 0. Diantara suku banyak
berikut yang memenuhi keriteria sebagai P (x) adalah ....

Tidak ada komentar:
Posting Komentar