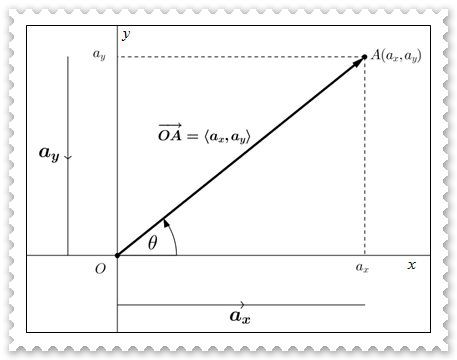
Contoh Soal Sudut antara Dua Vektor - Pada topik sebelumnya, kita telah belajar tentang perkalian skalar dua vektor. Pada topik tersebut, kita telah menyinggung sedikit tentang sudut antara dua vektor. Sebelum membahas lebih jauh tentang sudut antara dua vektor, apakan kalian masih ingat dengan gambar di bawah ini?
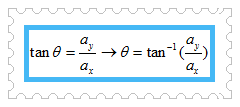
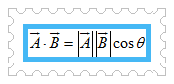
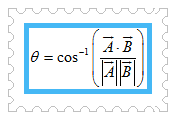
Tentang:
Index
Matematika Ipa kelas 12

Ya, gambar di atas telah kalian jumpai pada topik penjumlahan, pengurangan, dan panjang vektor. Jika vektor membentuk sudut θ terhadap sumbu x positif dan komponen dari vektor diketahui, maka kita dapat dengan mudah menghitung besar sudut θ. Perhitungan sudut θ dapat kita lakukan dengan memanfaatkan ilmu trigonometri dasar, yaitu dengan invers tangen sudut θ berikut ini.
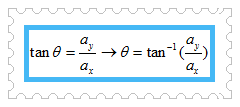
Cukup sederhana bukan? Nah, bagaimana jika sudut yang akan ditentukan berada di antara dua vektor? Misalnya sudut antara vektor dan yang komponen keduanya diketahui? Untuk mengetahui jawabannya, mari simak topik ini dengan saksama.
♕ KONSEP
▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩
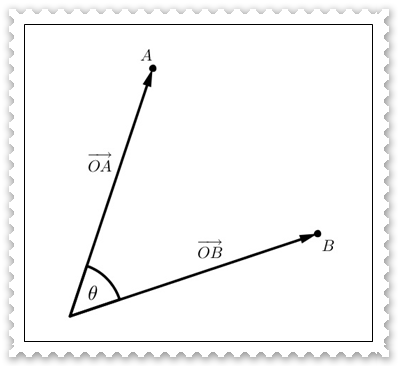
Perhatikan gambar di bawah ini.

Pada dimensi 2 dan 3, penentuan sudut antara dua vektor seperti gambar di atas dapat dilakukan dengan cara menggambar vektor-vektor pada koordinat Cartesius, kemudian mengukurnya dengan alat ukur sudut. Namun, cara ini tidak dapat lagi dilakukan pada dimensi yang lebih tinggi. Oleh karena itu, kita memerlukan suatu cara untuk menentukan besar sudut antara dua vektor secara umum.
Setelah mempelajari konsep tentang perkalian skalar dua vektor pada topik sebelumnya, kalian tentu masih ingat dengan definisi perkalian skalar antara dua vektor berikut ini.
Jika dan vektor-vektor tak nol dan θ sudut di antara vektor dan , maka perkalian skalar dari kedua vektor ini dapat didefinisikan dengan:
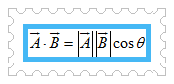
Dari definisi tersebut, dapat kita peroleh:
Dari persamaan di atas, dapat kita simpulkan bahwa untuk menentukan besar sudut antara dua vektor dapat dilakukan dengan menghitung invers dari kosinus berikut.
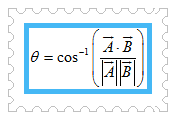
Kelebihan dari persamaan terakhir ini adalah kita dapat menghitung besar sudut antara dua vektor dalam dimenesi berapapun. Selama kedua vektor dinyatakan dalam komponen vektor, maka penentuan besar sudut antara keduanya selalu mungkin dilakukan.
SOAL 1
Jika kosinus dari suatu sudut lancip bernilai , maka besar sudut lancip tersebut adalah ….
SOAL 2
Besar sudut antara dua vektor tak nol dan dapat dihitung dengan menggunakan persamaan ….
SOAL 3
Misalkan dan vektor-vektor pada ruang dimensi dua. Jika hasil perkalian skalar dan adalah 2, serta panjang dan masing-masing 2, maka sudut yang terbentuk antara kedua vektor tersebut adalah ….
SOAL 4
Besar sudut antara vektor dan adalah ….
SOAL 5
Besar sudut antara vektor dan adalah….
SOAL 6
Besar sudut antara vektor dan adalah ….
SOAL 7
Sudut yang terbentuk antara vektor dan adalah ….
SOAL 8
Diketahui dan . Jika sudut antara kedua vektor merupakan sudut lancip dengan nilai tangen , maka hasil perkalian skalar kedua vektor tersebut adalah ….
SOAL 9
Sebuah persegipanjang ABCD memiliki panjang 3 satuan dan lebar 1 satuan. Besar sudut BAC pada persegipanjang tersebut adalah ….
SOAL 10
Pada kubus satuan ABCD.EFGH, besar sudut FAG adalah ….

Tidak ada komentar:
Posting Komentar