Contoh Soal Volume Benda Putar Mengelilingi Sumbu X

Contoh Soal Volume Benda Putar Mengelilingi Sumbu X - Pada topik sebelumnya, kalian telah menggunakan integral tertentu untuk menghitung luas daerah. Hal ini tidak mengherankan karena integral tertentu memang diciptakan untuk keperluan itu. Selain untuk menghitung luas daerah, ternyata integral tertentu dapat juga digunakan untuk memecahkan persoalan lainnya. Salah satunya volume benda putar.

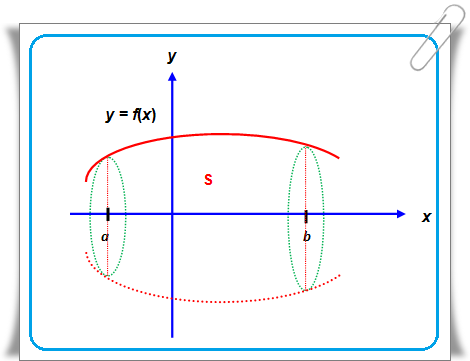
Perhatikan gambar berikut.

                            

        Misalkan daerah S dibatasi oleh kurva y = f(x), sumbu X, garis x = a, garis x = b, dengan a < b diputar mengelilingi sumbu X sebesar 360°. Untuk mendapatkan volume benda putar tersebut, dibuatlah potongan tabung-tabung kecil sebagai pendekatan volume benda. Jika jari-jari potongan tabung kecil itu y dan tingginya δx, maka:

                                                               δV=πy2δx$\delta V=\pi y^2\delta x$

Volume benda putar tersebut merupakan jumlah potongan tabung-tabung itu, sehingga:

                                                               V=∑i=1nπyi2δxi$V=\sum _{i=1}^n\pi {y_i}^2\delta x_i$

dengan n jumlah potongan tabung.

Untuk δx yang cukup kecil, akan dihasilkan pendekatan volume yang sempurna, yaitu:

                                                               V=limδx→0$V=\underset{\delta x\to 0}{lim}$ ∑i=1nπyi2δxi$\sum _{i=1}^n\pi {y_i}^2\delta x_i$

Bentuk limit di atas dapat dinyatakan dalam bentuk integral:

                                                               V=π∫aby2dx$V=\pi \underset{a}{\overset{b}{\int }}{y}^{2}dx$

Oleh karena y = f(x), maka bentuk tersebut dapat pula ditulis sebagai:

                                                               V=π∫ab(f(x))2dx$V=\pi \underset{a}{\overset{b}{\int }}{(f(x))}^{2}dx$

                

SOAL 1

Apabila daerah yang dibatasi oleh setengah lingkaran dan diameternya yang berimpit dengan sumbu X diputar 360° mengelilingi diameternya itu, maka benda putar yang terbentuk berupa ….

SOAL 2

Benda putar berbentuk kerucut dapat diperoleh dari ….

SOAL 3

Volume benda putar yang terjadi jika daerah yang dibatasi oleh parabola y2 = 2x, garis x = 4, dan sumbu X diputar 360° mengelilingi sumbu X adalah … satuan volume.

SOAL 4

Jika daerah yang dibatasi oleh grafik f(x) = 4 – x2 , sumbu X, dan sumbu Y diputar 360° terhadap sumbu X, maka volume benda putar yang terjadi adalah … satuan volume.

SOAL 5

Jika daerah yang dibatasi oleh grafik g(x) = 2x – x2dan sumbu X diputar 360° terhadap sumbu X, maka volume benda putar yang terjadi adalah … satuan volume.

SOAL 6

Daerah di kuadran III yang dibatasi oleh seperempat lingkaran x2 + y2 = 81 diputar 360° mengelilingi sumbu X. Volume benda putar yang terjadi dapat dinyatakan dengan ….

SOAL 7

Daerah yang dibatasi oleh kurva xy = 8, x = 1, x = 8, dan sumbu X diputar 360° mengelilingi sumbu X. Volume benda putar yang terjadi adalah … satuan volume.

SOAL 8

Daerah yang dibatasi oleh kurva 16x2 + 25y2 = 400 dan sumbu X diputar 360° mengelilingi sumbu X. Volume benda putar yang terjadi adalah … satuan volume.

SOAL 9

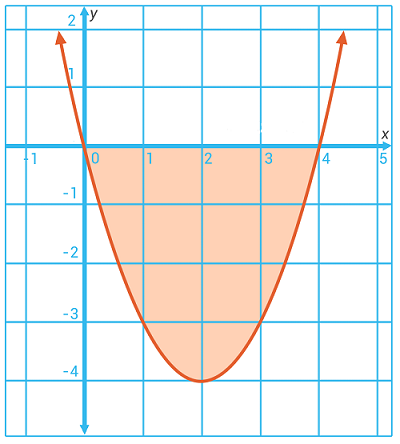
Perhatikan daerah yang diwarnai dengan warna merah pada gambar berikut ini.

Jika daerah tersebut diputar sebesar 360° mengelilingi sumbu X, volume benda putar yang terjadi adalah … satuan volume.

SOAL 10

Jika daerah yang dibatasi oleh grafik g(x) = sin 2x dan sumbu X diputar 360° terhadap sumbu X pada selang 0≤x≤π2$0\le x\le \frac{\pi }{2}$, maka volume benda putar yang terjadi adalah … satuan volume.

Tentang: Matematika Ipa kelas 12

Share:

Artikel Terkait