Contoh Soal Fungsi - Relasi dari himpunan A ke himpunan B adalah suatu aturan yang memasangkan anggota-anggota himpunan A dengan anggota-anggota himpunan B.
Tentang:
Matematika
Pengertian Fungsi atau Pemetaan
Fungsi (pemetaan) dari himpunan A ke himpunan B adalah relasi khusus yang memasangkan setiap anggota himpunan A dengan tepat satu anggota himpunan B.
✎Contoh 1
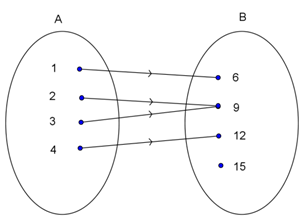
Perhatikan diagram panah berikut.

Dari diagram di atas terlihat bahwa setiap anggota himpunan A dipasangkan dengan tepat satu anggota himpunan B dengan:
A = {1, 2, 3, 4} disebut daerah asal (domain).
B = {6, 9, 12, 15}disebut daerah kawan (kodomain).
Himpunan {6, 9, 12} disebut daerah hasil (range).
B = {6, 9, 12, 15}disebut daerah kawan (kodomain).
Himpunan {6, 9, 12} disebut daerah hasil (range).
Syarat suatu relasi merupakan fungsi atau pemetaan adalah:
- setiap anggota himpuan A mempunyai pasangan di himpunan B.
- setiap anggota A dipasangkan dengan tepat satu anggota himpunan B.
Cara Menyajikan Suatu Fungsi (Pemetaan)
Sama halnya dengan relasi, fungsi dapat dinyatakan dengan 3 cara yaitu diagram panah, diagram kartesius, dan himpunan pasangan berurutan.
✎Contoh 2
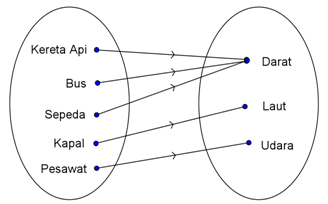
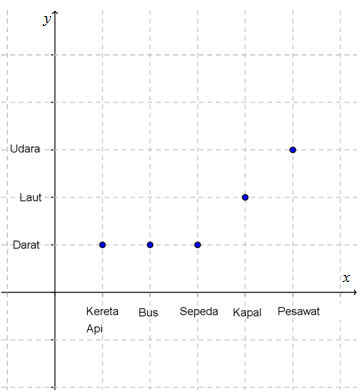
Berdasarkan gambar (1), himpunan alat-alat transportasi adalah kereta api, bus, sepeda, kapal, dan pesawat. Himpunan jalur transportasi digunakan adalah udara, darat, dan laut. Relasi dari himpunan alat-alat transportasi dengan himpunan jalurnya, merupakan sebuah fungsi. Nyatakan fungsi tersebut dengan cara diagram panah, diagram kartesius, dan diaggram panah.
Penyelesaian:
- Diagram Panah

- Diagram Kartesius

- Himpunan pasangan berurutan = {(kereta api, darat), (bus, darat), (sepeda, darat), (kapal, laut), (pesawat, udara)}
Banyak Fungsi (Pemetaan)
Jika banyak himpunan P adalah n (P) = p dan banyak anggota himpunan Q adalah n (Q) = q, maka banyak fungsi (pemetaan) dari:
- himpunan P ke Q adalah qp.
- himpunan Q ke P adalah pq.
✎Contoh 3
Jika himpunan P = {-1, 1} dan Q = {e, f, g, h, i}, maka tentukan banyak fungsi (pemetaan) himpunan P ke Q.
Penyelesaian:
Diketahui:
P = {-1, 1}, n (P) = p = 2
Q = {e, f, g, h, i}, n (Q) = q = 5
P = {-1, 1}, n (P) = p = 2
Q = {e, f, g, h, i}, n (Q) = q = 5
Banyak fungsi dari himpunan P ke Q = qp
Jadi, banyak fungsi dari himpunan P ke Q = 52 = 25.
✎Contoh 4
Jika himpunan P = {-1, 1} dan Q = {e, f, g, h, i}, maka tentukan banyak fungsi (pemetaan) himpunan Q ke P.
Penyelesaian:
Diketahui:
P = {-1, 1}, n (P) = p = 2
Q = {e, f, g, h, i}, n (Q) = q = 5
P = {-1, 1}, n (P) = p = 2
Q = {e, f, g, h, i}, n (Q) = q = 5
Banyak fungsi dari himpunan Q ke P = pq
Jadi, banyak fungsi dari himpunan Q ke P = 25 = 32.
S1
Pilihan Tunggal
Fungsi adalah ....
S2
Pilihan Tunggal
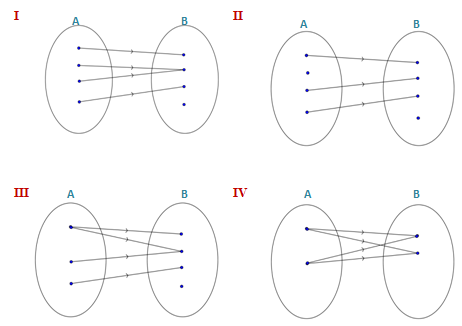
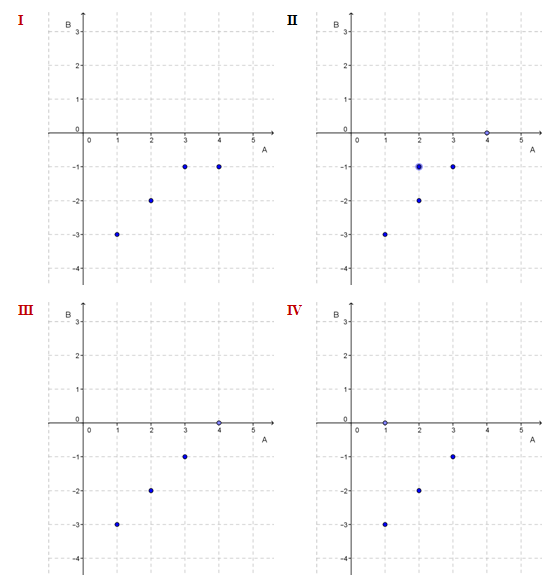
Perhatikan diagram-diagram panah berikut.

Diagram panah yang menyatakan suatu fungsi adalah ....
S3
Pilihan Tunggal
Diketahui P = {2, 4, 6, 8, 10} dan Q = {a, i, u, e, o}. Himpunan pasangan berurutan berikut yang merupakan fungsi adalah ....
S4
Pilihan Tunggal
Diketahui A = {1, 2, 3, 4} dan B = {-3, -2, -1, 0, 1, 2, 3}. Perhatikan diagram Cartesius berikut ini.

Diagram kartesius yang merupakan fungsi adalah ....
S5
Pilihan Tunggal
Domain pada fungsi {(1, 3), (3, 5), (5, 7), (7, 9)} adalah ....
S6
Pilihan Tunggal
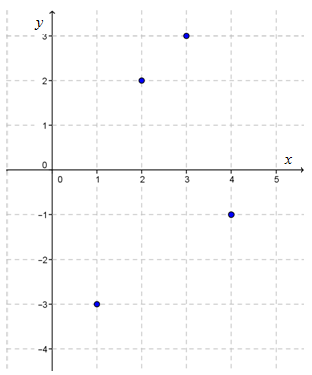
Perhatikan diagram kartesius berikut.

Daerah hasil (range) dari fungsi yang ditunjukan diagram kartesius di atas adalah ....
S7
Pilihan Tunggal
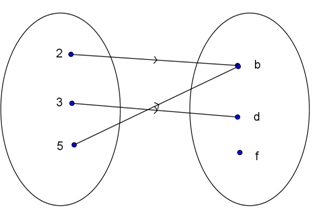
Perhatikan diagram panah berikut.

Daerah kawan (kodomain) dari fungsi yang ditunjukkan pada diagram panah di atas adalah ....
S8
Pilihan Tunggal
Diketahui:
A = {x | 11 < x ≤ 19, x bilangan prima}
B = {y | y3 < 30, y bilangan asli}
A = {x | 11 < x ≤ 19, x bilangan prima}
B = {y | y3 < 30, y bilangan asli}
Banyak semua fungsi yang mungkin dari himpunan B ke himpunan A adalah ....
S9
Pilihan Tunggal
Diketahui :
P = {bilangan prima antara 1 dan 10}
Q = {bilangan kelipatan 3 antara 1 dan 10}
P = {bilangan prima antara 1 dan 10}
Q = {bilangan kelipatan 3 antara 1 dan 10}
Banyak semua fungsi yang mungkin dari himpunan Q ke P adalah ....
S10
Pilihan Tunggal
Diketahui :
X = {bilangan genap antara 7 dan 17}
Y = {bilangan prima antara 1 dan 6}
X = {bilangan genap antara 7 dan 17}
Y = {bilangan prima antara 1 dan 6}
Banyak semua fungsi yang mungkin dari himpunan X ke Y adalah ...

Tidak ada komentar:
Posting Komentar