Contoh Soal Korespondensi Satu-Satu - Pada topik ini, kita akan mempelajari tentang korespondensi satu-satu. Konsep korespondensi satu-satu berhubungan erat dengan fungsi. Sebelum mempelajari tentang korserpondensi satu-satu kamu harus memahami terlebih dahulu tentang pengertian fungsi. Apakah kamu masih ingat tentang pengertian fungsi? Fungsi (pemetaan) dari himpuan A ke himpunan B adalah relasi khusus yang memasangkan setiap anggota A dengan tepat satu anggota himpunan B. Selanjutnya, mari simak ilustrasi berikut.





Tentang:
Matematika
Di setiap kelas, masing-masing siswa tentunya memiliki peringkat kelas yang berbeda. Ini akan membentuk relasi peringkatkarena satu siswa memiliki satu peringkat, begitu juga sebaliknya setiap peringkat hanya dimiliki oleh satu siswa. Relasi dari himpunan siswa ke himpunan peringkat dapat digambarkan pada diagram panah berikut ini.

Pada diagram panah 1, setiap anggota himpunan A berpasangan dengan tepat satu anggota himpunan B, sehingga dapat disebut sebagai fungsi atau pemetaan. Sebaliknya, setiap anggota himpunan B juga dapat dipasangkan dengan tepat satu anggota himpunan A seperti pada diagram panah 2.

Fungsi atau pemetaan bolak-balik yang ditunjukan oleh diagram panah 1 dan 2 disebut dengan korespondensi satu-satu.Mari pahami lebih lanjut tentang korespondensi satu-satu melalui uraian berikut.
Pengertian Korespondensi Satu-Satu
Korespondensi satu-satu adalah fungsi yang memetakan setiap anggota dari himpunan A ke tepat satu anggota B dan setiap anggota himpuan B ke tepat satu anggota A. ini berarti, banyak anggota himpunan A dan B harus sama atau n (A) = n (B).
◙ ◙ ◙ Contoh 1 ◙ ◙ ◙
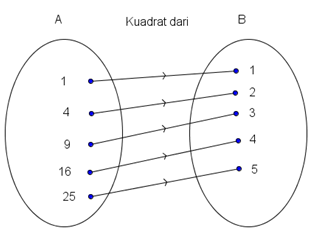
Diketahui A = {1, 4, 9, 16, 25} dan B = {1, 2, 3, 4, 5}. Gambarkan diagram panah dari himpunan A ke himpunan B dengan relasi kuadrat dari. Apakah fungsi dari himpunan A ke himpunan B merupakan korespondensi satu-satu?
Penyelesaian:
Diagram panah dari himpunan A ke himpunan B adalah sebagai berikut.

Berdasarkan pengertian korespondensi satu-satu, fungsi dari himpunan A ke himpunan B merupakan korespondensi satu-satu.
◙ ◙ ◙ Contoh 2 ◙ ◙ ◙
Diketahui P = {14, 16, 18, 20} dan Q = {12, 14, 16}. Nyatakan himpunan pasangan berurutan relasi dua lebihnya dari dari himpunan P ke himpunan Q. Apakah fungsi dari himpunan P ke himpunan Q merupakan korespondensi satu-satu?
Penyelesaian:
Diketahui:
P = {14, 16, 18, 20}
Q = {12, 14, 16}
P = {14, 16, 18, 20}
Q = {12, 14, 16}
Himpunan pasangan berurutan relasi dua lebihnya dari dari himpunan P ke himpunan Q adalah:
{(14, 12), (16, 14), (18, 16)}.
{(14, 12), (16, 14), (18, 16)}.
Berdasarkan pengertian korespondensi satu-satu, fungsi dari himpunan P ke himpunan Q bukan merupakan korespondensi satu-satu. Ini karena ada 1 anggota himpunan P yaitu 20 tidak memiliki pasanngan dengan anggota himpunan Q.
Banyak Korespondensi Satu-Satu
Jika n (A) = n (B) = n, maka banyak korespondensi satu-satu yang mungkin antara himpunan A dan B adalah:
n × (n - 1) × (n - 2) × ... × 3 × 2 × 1
Contoh:
- Jika n (A) = n (B) = n = 3, maka banyak korenspondensi satu-satu yang mungkin antara himpunan A dan B adalah:
3 × 2 × 1 = 6 - Jika n (A) = n (B) = n = 4, maka banyak korenspondensi satu-satu yang mungkin antara himpunan A dan B adalah:
4 × 3 × 2 × 1 = 24
◙ ◙ ◙ Contoh 3 ◙ ◙ ◙
Berdasarkan contoh 1, berapa banyak korespondensi satu-satu yang mungkin antara himpunan A dan himpunan B?
Penyelesaian:
Diketahui :
A = {1, 4, 9, 16, 25}
B = {1, 2, 3, 4, 5}
n (A) = n (B) = n = 5
A = {1, 4, 9, 16, 25}
B = {1, 2, 3, 4, 5}
n (A) = n (B) = n = 5
Banyak korespondensi satu-satu yang mungkin antara himpunan A dan himpunan B adalah:
5 × 4 × 3 × 2 × 1 = 120.
5 × 4 × 3 × 2 × 1 = 120.
Jadi, banyak korespondensi satu-satu yang mungkin antara himpunan A dan himpunan B adalah 120.
S1
Pilihan Tunggal
Korespondensi satu-satu adalah ....
S2
Pilihan Tunggal
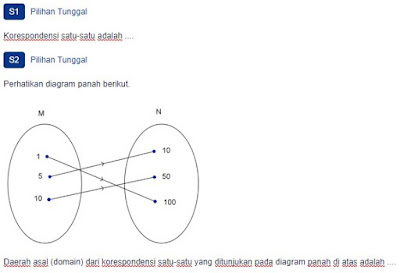
Perhatikan diagram panah berikut.

Daerah asal (domain) dari korespondensi satu-satu yang ditunjukan pada diagram panah di atas adalah ....
S3
Pilihan Tunggal
Perhatikan diagram-diagram panah berikut.

Korespondensi satu-satu ditunjukkan oleh diagram panah ....
S4
Pilihan Tunggal
Berikut ini yang merupakan korespondensi satu-satu adalah ....
S5
Pilihan Tunggal
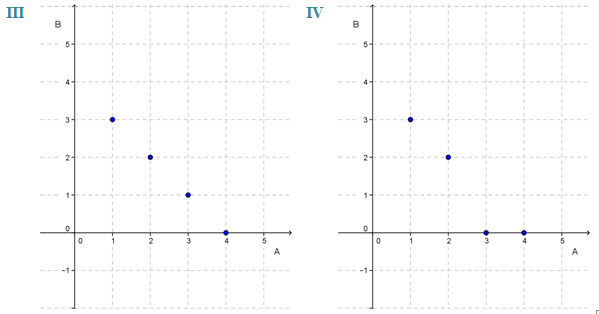
Perhatikan diagram kartesius berikut ini.


Diagram kartesius yang merupakan korespondensi satu-satu adalah ....
S6
Pilihan Tunggal
Perhatikan pernyataan-pernyataan berikut.
I. Setiap relasi adalah fungsi.
II. Setiap fungsi adalah relasi.
III. Setiap fungsi adalah korespondensi satu-satu.
IV. Setiap korespondensi satu-satu adalah fungsi.
II. Setiap fungsi adalah relasi.
III. Setiap fungsi adalah korespondensi satu-satu.
IV. Setiap korespondensi satu-satu adalah fungsi.
Dari pernyataan-pernyataan di atas, yang merupakan pernyataan yang salah adalah ....
S7
Pilihan Tunggal
Diketahui pernyataan-pernyataan berikut.
(1) Negara dengan ibukotanya.
(2) Provinsi dengan ibukotanya.
(3) Siswa dengan tempat duduknya.
(4) Siswa dengan nilainya.
(2) Provinsi dengan ibukotanya.
(3) Siswa dengan tempat duduknya.
(4) Siswa dengan nilainya.
Pernyataan yang merupakan contoh korespondensi satu-satu adalah ....
S8
Pilihan Tunggal
Diketahui:
A = {x | 11 < x < 20, x bilangan prima}
B = {y | y3 < 30, y bilangan cacah}
A = {x | 11 < x < 20, x bilangan prima}
B = {y | y3 < 30, y bilangan cacah}
Banyak semua korespondensi satu-satu yang mungkin antara himpunan A dan B adalah ....
S9
Pilihan Tunggal
Diketahui :
P = {bilangan prima antara 1 dan 10}
Q = {bilangan kelipatan 2 antara 1 dan 10}
P = {bilangan prima antara 1 dan 10}
Q = {bilangan kelipatan 2 antara 1 dan 10}
Banyak korespondensi satu-satu yang mungkin antara himpunan P dan Q adalah ....
S10
Pilihan Tunggal
Diketahui himpunan-himpunan berikut.
P = {x | x > 4, x bilangan asli}
Q = {x | x faktor prima dari 105}
R = {x | x > 4, x bilangan prima}
S = {x | 3 ≤ x ≤ 7, x bilangan ganjil}
Q = {x | x faktor prima dari 105}
R = {x | x > 4, x bilangan prima}
S = {x | 3 ≤ x ≤ 7, x bilangan ganjil}
Himpunan-himpunan yang dapat berkorespondensi satu-satu adalah ....
Tidak ada komentar:
Posting Komentar