Luas segitiga A =1/2absinC - Segitiga dapat diklasifikasikan berdasarkan sisi-sisi dan sudut yang dimilikinya.
Kita gunakan rumus ini ketika diketahui panjang dua sisi dan satu sudut.
Contoh 1
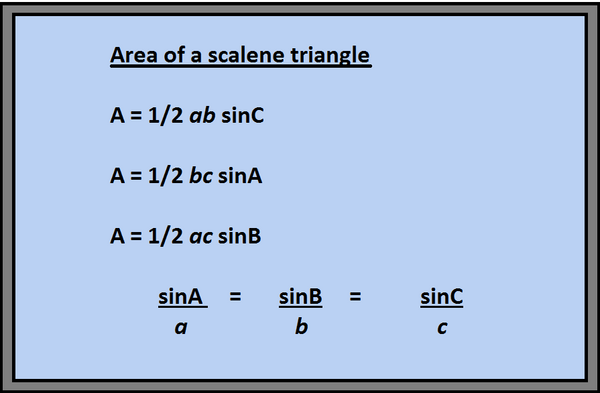
Nyatakan luas segitiga [gambar 204.2] bulatkan sampai satu tempat desimal.
∠PSR
cos P = 2.938/10
= 72.91∘
Karena itu sudut P= 54.01 + 72.91 = 126.92 ≃ 127
Luas daerah ∠PQR
Dengan menggunakan rumus A = 1/2QRsinP
A = 1/2 (10)(5)sin(127)
= 19.965 ≃ 20.0
Contoh 3
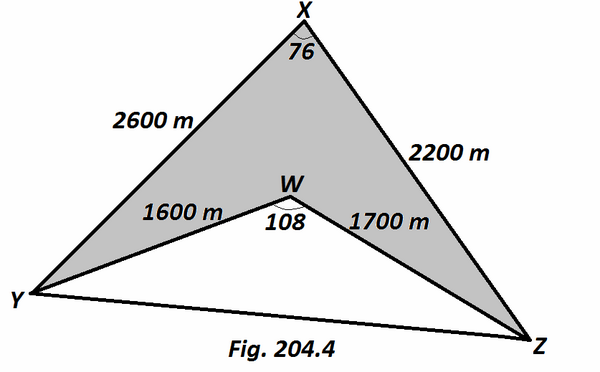
Nyatakan luas daerah yang diarsir dalam hektar. (1 hektar = 10 000 m2) [Gambar 204.4]
A = 1/2yzsinX
= 1/2 (2200)(2600)sin(76)
= 2775045.77 ≃ 2775046m2
∠WYZ
A = 1/2yzsinW
= 1/2 (1700)(1600)sin(108)
= 1293436.86 ≃ 1293437m2
Luas daerah yang diarsir XWYZ =2775046 - 1293437 = 1481609m2 ≃ 148.1 ha
Tentang:
Matematika
 |
| Luas segitiga A =1/2absinC |
Sudut-sudut dalam sebuah segitiga apabila dijumlahkan selalu berjumlah 180∘.
Jenis-jenis segitigaSegitiga sama sisi, segitiga sama kaki, segitiga sebarang, segitiga lancip, segitiga siku-siku, segitiga tumpul.
Jenis-jenis segitigaSegitiga sama sisi, segitiga sama kaki, segitiga sebarang, segitiga lancip, segitiga siku-siku, segitiga tumpul.
((Dalam pelajaran ini kita hanya akan mambahas tentang segitiga sebarang.))
"Segitiga sebarang adalah segitiga yang ketiga sisinya memiliki panjang berbeda dan besar setiap sudut dalamnya tidak sama ".
Luas segitiga
Luas segitiga adalah 1/2 (alas) (tinggi) = 1/2 bh
"Segitiga sebarang adalah segitiga yang ketiga sisinya memiliki panjang berbeda dan besar setiap sudut dalamnya tidak sama ".
Luas segitiga
Luas segitiga adalah 1/2 (alas) (tinggi) = 1/2 bh

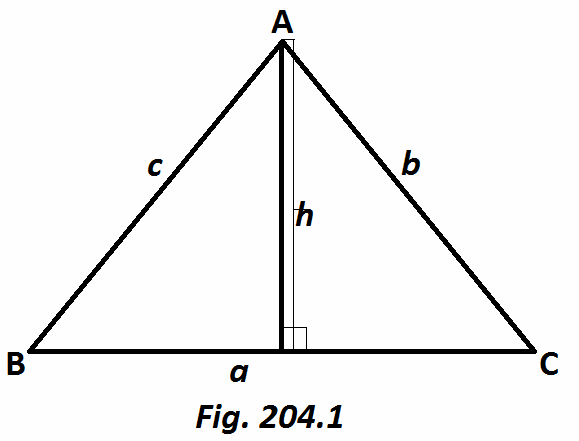
Dari Gambar 204.1,
Dengan aturan sinus, kita dapatkan
Dengan aturan sinus, kita dapatkan
sinC = h/b, di mana h adalah tinggi segitiga,
h = bsinC
Karena luas segitiga adalah 1/2bh = 1/2absinC.
h = bsinC
Karena luas segitiga adalah 1/2bh = 1/2absinC.
Kita gunakan rumus ini ketika diketahui panjang dua sisi dan satu sudut.
Contoh 1
Nyatakan luas segitiga [gambar 204.2] bulatkan sampai satu tempat desimal.


A 5.2 cm2
B 5.1 cm2
C 5.0 cm2
D 5.3 cm2
E 5.29 cm2
Jawaban C
Penjelasan
Jawaban C
Penjelasan
Dengan menggunakan rumus A = 1/2 ac sinB
A = 1/2 (4.6)(2.3)[sin(72)]
= 1/2 (4.6)(2.3)(0.951)
= 5.031 ≃ 5.0 cm2
Contoh 2
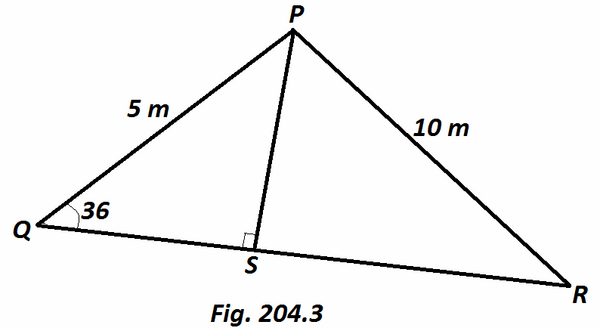
Nyatakan luas segitiga dalam m2 (bulatkan sampai satu tempat desimal). [Gambar 204.3]
A = 1/2 (4.6)(2.3)[sin(72)]
= 1/2 (4.6)(2.3)(0.951)
= 5.031 ≃ 5.0 cm2
Contoh 2
Nyatakan luas segitiga dalam m2 (bulatkan sampai satu tempat desimal). [Gambar 204.3]

A 14.5 m2
B 19.0 m2
C 14.7 m2
D 20.0 m2
E 19.6 m2
Jawaban D
Penjelasan
Perhatikan bahwa sudut yang bersangkutan tidak diketahui yaitu, sudut P. Jadi kita mencari sudut pertama dan kemudian menghitung luas segitiga.
∠ PQS
∠PQS
sin36 = PS/5,
jadi PS = 5sin36
= 2.938 m.
Kemudian, cos P = 2.938/5
P= 54.01∘.
B 19.0 m2
C 14.7 m2
D 20.0 m2
E 19.6 m2
Jawaban D
Penjelasan
Perhatikan bahwa sudut yang bersangkutan tidak diketahui yaitu, sudut P. Jadi kita mencari sudut pertama dan kemudian menghitung luas segitiga.
∠ PQS
∠PQS
sin36 = PS/5,
jadi PS = 5sin36
= 2.938 m.
Kemudian, cos P = 2.938/5
P= 54.01∘.
∠PSR
cos P = 2.938/10
= 72.91∘
Karena itu sudut P= 54.01 + 72.91 = 126.92 ≃ 127
Luas daerah ∠PQR
Dengan menggunakan rumus A = 1/2QRsinP
A = 1/2 (10)(5)sin(127)
= 19.965 ≃ 20.0
Contoh 3
Nyatakan luas daerah yang diarsir dalam hektar. (1 hektar = 10 000 m2) [Gambar 204.4]

A 148.0 ha
B 195.0 m2
C 148.1 ha
D 148.1 m2
E 618.2 ha
Jawaban C
Penjelasan
Dalam hal ini kita akan mempertimbangkan dua segitiga secara terpisah dan kemudian menemukan luas daerah yang diarsir dengan mengurangi luas segitiga lebih besar dengan yang lebih kecil.
∠XYZ
B 195.0 m2
C 148.1 ha
D 148.1 m2
E 618.2 ha
Jawaban C
Penjelasan
Dalam hal ini kita akan mempertimbangkan dua segitiga secara terpisah dan kemudian menemukan luas daerah yang diarsir dengan mengurangi luas segitiga lebih besar dengan yang lebih kecil.
∠XYZ
A = 1/2yzsinX
= 1/2 (2200)(2600)sin(76)
= 2775045.77 ≃ 2775046m2
∠WYZ
A = 1/2yzsinW
= 1/2 (1700)(1600)sin(108)
= 1293436.86 ≃ 1293437m2
Luas daerah yang diarsir XWYZ =2775046 - 1293437 = 1481609m2 ≃ 148.1 ha
Tidak ada komentar:
Posting Komentar