Penerapan Aturan Transformasi Geometri - Pada topik sebelumnya kalian telah belajar menganalisis sifat-sifat transformasi geometri (translasi, refleksi garis, dilatasi, dan rotasi) dengan pendekatan koordinat dan menerapkannya dalam menyelesaikan masalah matematika. Pada topik kali ini kalian akan belajar menyelesaikan masalah nyata yang berkaitan dengan transformasi geometri.
Sebelumnya, mari kita ingat kembali sifat-sifat objek yang mengalami transformasi geometi seperti refleksi (penceminan), translasi (pergeseran), dilatasi (perbesaran), dan rotasi (perputaran). Kita akan menggunakan sifat-sifat tersebut untuk menyelesaikan masalah-masalah nyata.
Contoh 1 :
Contoh 2 :
Contoh 3 :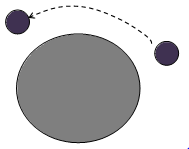
Contoh 4 :
Contoh 5 :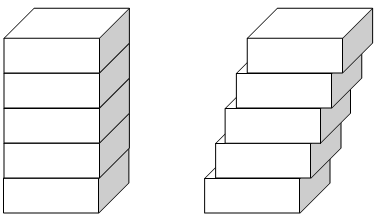
Nah, itu tadi beberapa contoh terapan transformasi geometri dalam kehidupan sehari-hari. Agar lebih jelas silakan kerjakan soal-soal yang tersedia. Selamat belajar!
Tentang:
Matematika
 |
| Penerapan Aturan Transformasi Geometri |
Sebelumnya, mari kita ingat kembali sifat-sifat objek yang mengalami transformasi geometi seperti refleksi (penceminan), translasi (pergeseran), dilatasi (perbesaran), dan rotasi (perputaran). Kita akan menggunakan sifat-sifat tersebut untuk menyelesaikan masalah-masalah nyata.
Contoh 1 :
Kalau kalian perhatikan, ada beberapa huruf yang memenuhi sifat refleksi, yaitu :

Coba kalian cermati huruf-huruf lain yang memiliki sifat refleksi.
Contoh 2 :
Apakah kalian pernah ke mall atau hotel berbintang?
Pada kedua tempat tersebut, kalian tentu akan menemukan eskalator ataupun lift yang akan memindahkan kalian dari lantai bawah ke lantai atasnya atau sebaliknya.
Menurut kalian, eskalator atau lift yang dapat memindahkan orang dari lantai tertentu ke lantai yang lain menggunakan sifat trasformasi geometri apa?
Penyelesaian :
Kalau kita perhatikan perpindahan orang dari satu lantai ke lantai yang lain tidak mengalami perbesaran atau pengecilan orang, berarti bukan dilatasi. Orang tersebut juga tidak mengalami perubahan arah hadap, berarti bukan pencerminan, bukan pula rotasi. Eskalator atau lift hanya memindahkan orang ke tempat yang berbeda. Dengan demikian, transformasi yang bersesuaian dengan gerak eskalator atau lift adalah translasi.
Contoh 3 :
Pernahkah kalian melihat orbit bulan terhadap bumi?

Gerakan bulan mengelilingi bumi menggunakan sifat transformasi rotasi.
Contoh 4 :
Pernahkan kalian rekreasi ke Candi Borobudur atau candi-candi yang lain?
Di taman rekreasi Candi Borobudur kalian akan menemukan miniatur candi yang terbuat dari tanah liat atau bahan lain. Pembuatan miniatur candi menggunakan sifat transformasi dilatasi dengan faktor skala k dimana 0 < k < 1
Contoh 5 :
Lima batu bata yang sama disusun dalam urutan vertikal. Kemudian tumpukan itu digeser dengan arah dan panjang yang sama, tanpa menggeser bata yang paling bawah.
Perhatikan gambar berikut!

Jika jarak pergeseran tiap batu bata yang berdekatan adalah 2 cm, tentukan panjang pergeseran batu bata kelima!
Penyelesaian :
Oleh karena batu bata paling bawah tetap, maka yang bergeser hanya empat batu bata.
Oleh karena jarak pergeseran antara batu bata yang berdekatan sama, maka panjang pergeseran batu bata adalah 4 x 2 cm = 8 cm.
Oleh karena jarak pergeseran antara batu bata yang berdekatan sama, maka panjang pergeseran batu bata adalah 4 x 2 cm = 8 cm.
Nah, itu tadi beberapa contoh terapan transformasi geometri dalam kehidupan sehari-hari. Agar lebih jelas silakan kerjakan soal-soal yang tersedia. Selamat belajar!
Tidak ada komentar:
Posting Komentar